Ebenen und Geraden?
Hallo zusammen!
Ich habe eine Frage zum Thema Ebenen und Gerade in der Mathematik. Es ist so: Ich soll ohne Rechnung begründen, wieso die Geraden g1 und g2 in der Ebene E liegen. Ich weiß auch auf jeden Fall, dass es so ist; aber mir fallen nicht die richtigen Worte für eine gute, richtige Begründung ein. Bei beiden Geraden sowie auch der Ebenengleichung ist der Stützvektor gleich, sprich: Beide Geraden schneiden diesen Punkt. Bei g1 ist nun der erste Richtungsvektor auch der erste der Ebenengleichung und bei g2 ist es der zweite Richtungsvektor der Ebenengleichung. Wie begründe ich das jetzt mathematisch korrekt und schön? :D
Anbei noch das Bild mit der konkreten Aufgabenstellung.
Danke schon mal im Voraus für jede Hilfe!!
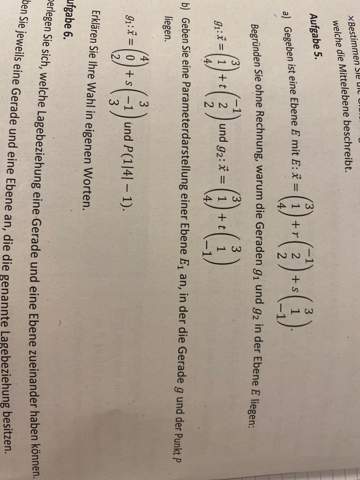
Aufgabe 5a) ist das. :)
3 Antworten
Die Ebene wird festgelegt durch einen Punkt und 2 richtungsvektoren
Bei der geraden brauchen wir nur 1 Punkt und eine richtung
Hier liegt der Punkt auf der Ebene und der richtungsvektor ist derselbe wie einer von der Ebene. Daher liegen die geraden drauf.
(um parallel zur Ebene zu sein, würde der Punkt woanders liegen, aber der richtungsvektor der der Ebene sein.
Und für einen Schnitt mit der Ebene hätte man einen Punkt auf der Ebene, aber eine völlig andere Richtung)
Die geraden Parameter + einem richtungsvektor durch den Punkt. Also einfach r mal davor schreiben
Also einfach nur r mal den Punkt P? Und wie begründe ich das?
Wenn das Skallarprodukt zwischen dem Normalenvektor der Ebene und den Richtungsvektoren der Geraden gleich 0 ist + die Ortsvektoren der Geraden auf der Ebene liegen ( Punktprobe), dann liegen die Geraden auf der Ebene.
weil die beiden geraden genau die ebene aufspannen.
Erstmal vielen Dank!!
Wie müsste ich das dann bei 5b) machen?