Wie kann man sich negative Exponenten vorstellen?
Die Lösungsformel für negative Exponenten ist klar: Der Kehrwert, also bei z.B. 2 hoch -3 wäre das 1 geteilt durch 2 hoch 3.
Doch wie kann man sich das anschaulich vorstellen? Für positive Exponenten kann man ja sagen: Die Basiszahl wird so oft mit sich selbst mal genommen wie es im Exponenten steht. 2 hoch 3 = 2 * 2 * 2.
5 Antworten
"Mit sich selbst multiplizieren" ist nur ein "Sonderfall" für ganze positive Exponenten.
Universell gilt für das Potenzieren (x hoch x = x^y):
x^y = pow(x,y) = e^(log(x)*y) = exp(log(x)*y)
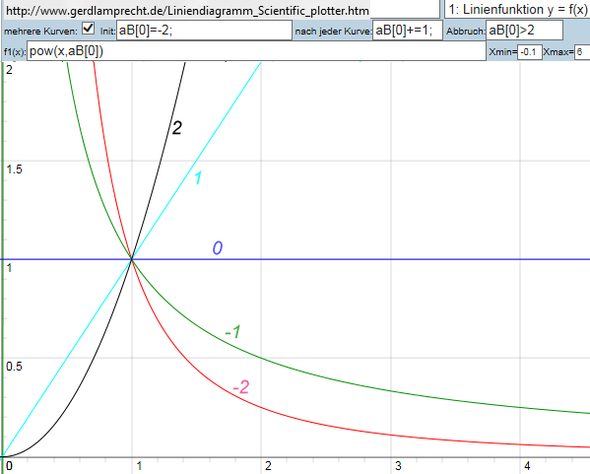
Wenn man sich die Linien anschaut, sieht man, dass alles stufenlos funktioniert. siehe Bild per
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
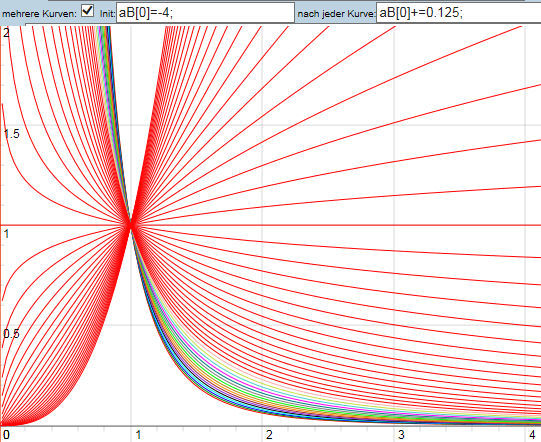
Natürlich kann man die Schritte beliebig verkleinern -> Bild 2
Siehe auch
für exaktes Berechnen von 1.3^0.7
Mir erscheint das immer etwas sinnvoller, wenn man sich mal ein Reihe ansieht:
2^4=16
2^3=8
2^2=4
2^1=2
2^0=1
2^-1=0,5
2^-2=0,25
2^-3=0,125
2^-4=0,0625
Der "Clou" dabei ist, dass n^0=1 ist.
Durch die Basiszahl wird so oft geteilt, wie es im Exponenten steht (teilen ist ja das "Gegenteil" von multiplizieren) , also 2^(-3)=(((1/2)/2)/2)
Formel einer Hyperbel y=f(x)= m/x mit m =konstant und x ist die unabhängige Variable
nun zu den Term y= 2^-x ergibt y=1/2^x hier ist m=1 und der Ausdruck 2^x
ist eigentlich 2^x=x der Unterschied liegt in der Steilheit der kurve.
Beispiel : x=2 nun mit 2^2=4
a ^ (-n) = 1 / (a ^ n)
Du rechnest also a ^ n wie immer aus und führst dann noch die Rechnung 1 / a ^ n durch.
2 ^ -3 = 1 / (2 ^ 3)
2 ^ 3 = 8
1 / (2 ^ 3) = 1 / 8
Wenn du dir ein Bild davon machen willst, dann Wertetabelle aufstellen und zeichnen lassen.