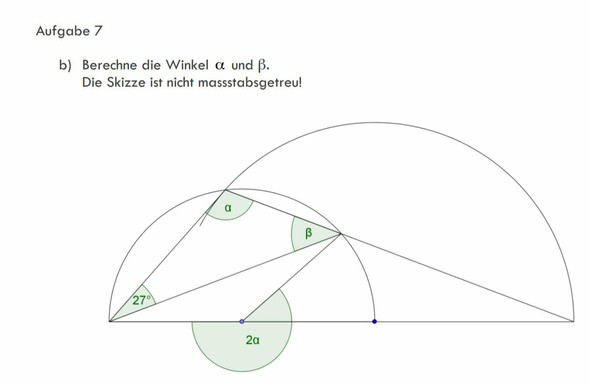
Wie kann man die Winkel herausfinden?
4 Antworten
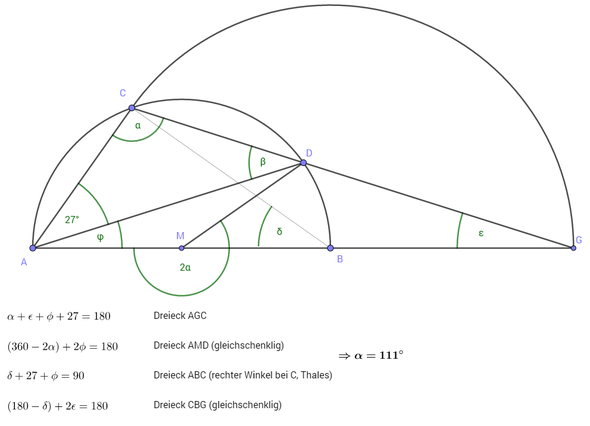
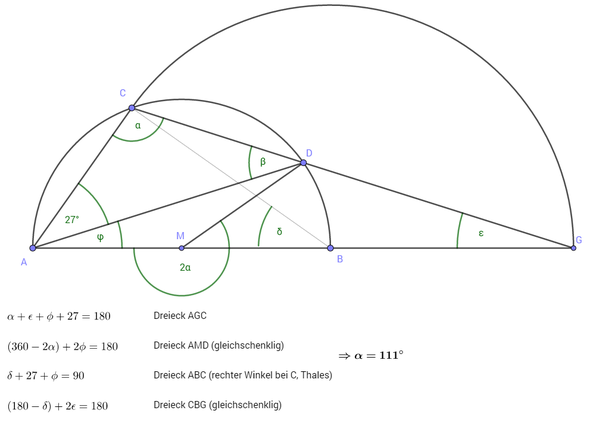
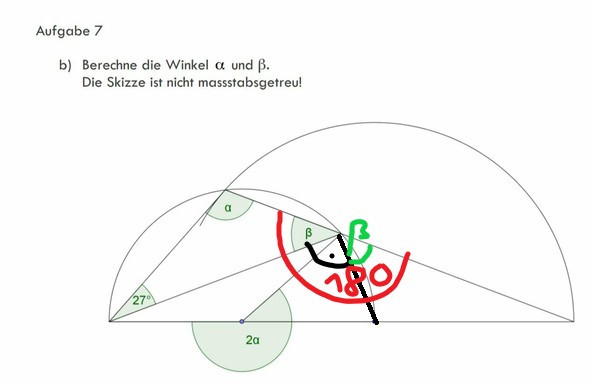
Man kann das im Wesentlichen alles aus dem Winkelsummensatz im Dreieck ableiten. Zusätlich benötigt man noch den Satz des Thales. Da das Ursprungsbild weder Punkte noch Hilfswinkel benannt hat, habe ich ein weiteres Bild angefertigt.
Man kommt auf vier (lineare Gleichungen) für vier Winkel, aus denen man dann alpha=111° errechnen kann. Damit ergibt sich beta = 42°.
[beta = delta nach dem Peripheriewinkelsatz, so spart man sich beta = 180 - 27 -alpha]
cos(27) = 0,89 (Verhältnis Ankathete / Hypotenuse (von 27°))
sin^-1(0,89) = 63 --> b = 63 (Gegen / Hypo (von b))
Gilt nur, wenn es rechtwinklig ist.
Demnach wäre also a = 90°
sieht irgendwie nicht rechtwinklig aus auch wenn die skizze nicht massstabsgetreu ist..
Offensichtlich? Es steht doch da, dass die Skizze NICHT maßstabsgetreu ist.
Nur dann wäre das untere eben kein Dreieck, aber naja, Skizze nicht Maßstabsgetreu :)
Bei dem neuen Dreieck ist ein rechter Winkel vorhanden.
Er ist genau so groß, wie 2 mal b
Also ist b = 45
Dann 180 - 27 - 45 = 108
Ich bin mir aber nicht sicher, ob es so geht
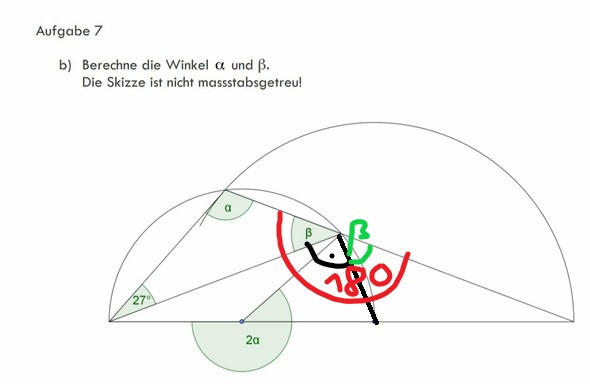
Ist es rechtwinklig?
Wenn alpha=90° wäre, müsste 2*alpha = 180° sein, es ist aber offensichtlich größer.
Mit Geogebra habe ich alpha = 111°, suche aber noch nach einer mathematischen Begründung