Wie kann man die Fakultät von großen Zahlen in Windows 10 berechnen?
Der normale Taschenrechner zeigt nur "Überlauf" an.
Freue mich auf Antworten.
4 Antworten
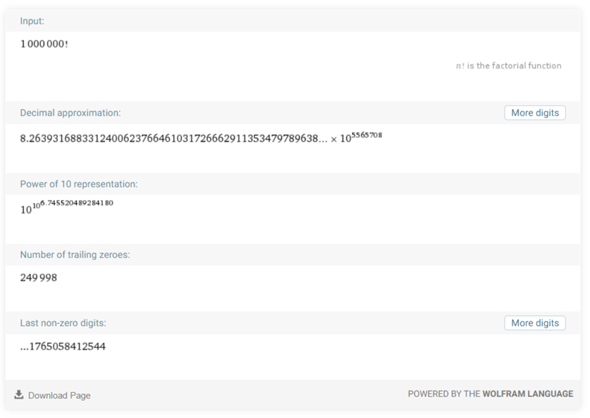
Wenn es dir nur um einzelne Werte geht, sollte https://www.wolframalpha.com/ ausreichen. WolframAlpha basiert auf Mathematica, ist quasi die Web-Version davon und hat auch mit 1.000.000! keine Probleme (müsste man testen, wie weit man es ausreizen kann).
Geht es tatsächlich um systematische Berechnungen von bestimmten Fakultäten, ist Python sicher keine schlechte Wahl (wenn auch nicht die effizienteste), weil du dir keine Gedanken über die Größe der Zahlen machen musst (Python operiert bis zu einem bestimmten Punkt dynamisch).
def fac(n):
if n == 0 or n == 1:
return 1
p = 1
for i in range(2, n+1):
p *= i
return p
Auch damit sind Fakultäten bis in die Millionen relativ fix berechenbar (wenn auch um Weiten langsamer als WolframAlpha). Die beiden Möglichkeiten decken in aller Regel die meisten Nutzungsgebiete ab.
Was willst du denn konkret berechnen? Bzw. wofür?

Wenn du sehr große Fakultäten berechnen willst, dann kannst du "NumberFactory" von Alexander Yee verwenden:
https://github.com/Mysticial/NumberFactory
müsstest du jedoch mit Visual Studio kompilieren (Community Version reicht).
Als alternative könntest du auch Alexander Yees Programm y-cruncher nehmen und dir ne eigene Formel für Fakultät schreiben (hab jedoch noch nie getestet, ob Fakultäten in den "Custom Formulas" unterstützt werden), da das Programm für das Berechnen von mathematischen Konstanten erstellt wurde.
Du kannst z.B. bei Google die Zahlen berechnen, tippe dazu in das Suchfeld ein:
=111!
so wird dir die Fakultät von 111 berechnet.
Ich möchte weitaus größere Zahlen berechen. Geht das eventuell über die Kommandozeile?
Du kannst einen der im Internet verfügbaren Fakultätsrechner wie z.B.
verwenden.
Na, das ist ja eine echt niedrige Zahl. Vielleicht kann dir noch diese Seite weiter helfen:
http://www.luschny.de/math/factorial/FastFactorialFunctions.htm
Bereits für die von mir verlinkte Seite muß übrigens eine eigene Artihmetik programmiert werden. Mit der in den üblichen Programmiersprachen verwendeten Double Precision Artithmetik kommt man nämlich nur bis 170!
https://de.wikipedia.org/wiki/Fakult%C3%A4t_(Mathematik)#Rekursive_und_iterative_Berechnung
Danke, da kann man aber auch nicht mehr als 100.050 n! berechnen.