Wie kann ich eine symmatrische Matrix mithilfe einer Funktion herleiten?
Hallo, folgende Aufgabe:
gegeben g(x)= 5x^2+3y^2+2z^2-xy+8xz und
leiten Sie die symmetrische Matrix A her
Mein Problem ist, dass ich keinerlei Lösungsansatz habe. Da es sich um eine symmetrische Matrix handeln soll, weiß ich, dass es ausreicht, die Hauptdiagonale + die 3 Werte oberhalb unter unterhalb zu bestimmen.
Mein Ansatz wäre, die beiden Gleichungen, also g(x) und Q= x'Ax (wobei x' ein Vektor mit [x y z] ist) gleichzusetzen. Aber wie ich dann damit weiterrechne, verstehe ich nicht. Mir wurde gesagt ich könne die Werte auslesen, also dass a_11=5, a_22=3, a_33 = 2 sei und dann a_12= -1, da -xy das -1 ergibt. Aber selbst falls das stimmt, erkenne ich die Herangehensweise dahinter nicht und könnte es vermutlich nicht reproduzieren.
Ich wäre sehr dankbar, wenn mir jemand einen Richtungsweiser geben könnte, wie ich an so eine Aufgabe herangehen muss.
Vielen Dank
Woher kommen die Variablen y und z? Ist x links ein Vektor und rechts eine Komponente von x?
das war meine Vermutung. Aus der Aufgabenstellung (da steht lediglich die Glechung Q = x'Ax) ergibt sich das aber nicht direkt und könnte daher falsch sein.
4 Antworten
Deine Überlegungen sind bisher richtig! Tipp: Mache einen Ansatz für die gesuchte Matrix Q und bezeichne dabei die Einträge der Matrix wie gewohnt als q11, q12, ... und berechne x^T Q x. Du erhältst eine allgemeine quadratische Form mit den Einträgen der Matrix als Koeffizienten. Dann musst du nur noch einen Koeffizientenvergleich mit der gegebenen quadratischen Form g machen!
Doch, du hast völlig Recht! Aufpassen muss man nur bei den Mischtermen, da braucht es die Bedingung der Symmetrie, damit man die Matrix überhaupt eindeutig festlegen kann.
Verstehe. Aus einem Term wie Q(x)= 3x^2+6xz+y^2-4yz+8z^2 kann ich also, wenn ich Symmetrie annehme, die 3x3 Matrix
3 0 6
0 1 -4
6 -4 8
aufstellen. Muss ich Symmetrie unterstellen oder gibt es andere Wege aus diesem Term eine Matrix zu erhalten, die ggf. nicht symmetrisch ist? Ich frage, da ich in weiterführenden Aufgaben dann die Definitheit bestimmen muss, und die Determinante dieser Matrix ja negativ wäre, allerdings Positiv Definit als Ergebnis angegeben wurde. Daher denke ich, dass die aufgestellte Matrix falsch ist.
Nein, Vorsicht, wie ich schon bei einer anderen Antwort kommentiert habe: 6xz muss sich auf a13 und a31 verteilen, also sind die Einträge 3 statt 6. Genauso auch die anderen beiden: -2 statt -4.
Oh, ok. Bei der ursprünglich gestellten Aufgabe ergab sich aber aus -xy ja ein -1, anstatt ein -0,5 bei q_12 bzw q_21 und aus dem 8xz hatte ich dann auch 8 für q_31 und q_13 hergeleitet. War das dann falsch oder war es hier richtig aufgrund der Symmetrie und in der später gestellten Frage muss es aufgrund fehlender Symmetrie aufgeteilt werden?
Danke für die weiteren ausführlichen Erklärungen. Ich habe das Gefühl es gibt immer etwas, was ich nicht beachte bzw. kleine Unterschiede in den Gegebenheiten
Ja, das war leider falsch. Es muss ja q12+q21=-1 sein. Das kann passieren, indem q12=-1 und q21=0 ist, dann ist -1+0=-1. Oder es kann passieren, indem q12=5 und q21=-6 ist, denn 5-6=-1. Damit die Matrix symmetrisch ist, muss aber q12=q21=-0,5 sein, und auch dann ist -0,5-0,5=-1.
Alles klar. Dann ist es aber ja immer gleich. Vielen Dank nochmal für die ausführliche Hilfe
Genau, die Einträge sind wegen Symmetrie paarweise gleich!
Hallo Username123321,
Um die Matrix A zu bestimmen, kannst du den Ansatz verwenden, den du bereits erwähnt hast. Du möchtest die Funktion g(x) mit der quadratischen Form Q = x'Ax gleichsetzen. Um die Matrix A zu bestimmen, musst du die Koeffizienten der quadratischen Form Q identifizieren. In deinem Fall ist Q = 5x^2 + 3y^2 + 2z^2 - xy + 8xz. Um die Koeffizienten zu bestimmen, musst du die Terme in Q entsprechend den Elementen der Matrix A zuordnen. Die Hauptdiagonale der Matrix A entspricht den Koeffizienten der quadratischen Terme in Q. In deinem Fall sind a_11 = 5, a_22 = 3 und a_33 = 2. Die Werte oberhalb und unterhalb der Hauptdiagonale entsprechen den Koeffizienten der gemischten Terme in Q. In deinem Fall ist a_12 = -1, da der Term -xy in Q vorkommt. Indem du die Werte aus Q den entsprechenden Elementen der Matrix A zuordnest, erhältst du die symmetrische Matrix A.
Liebe Grüße
Vorsicht, a21+A12=-1, bei einer symmetrischen Matrix wäre also a12=a21=-0,5.
Du schreibst halt das Matrix-Vektor-Produkt ausgeschrieben mal hin
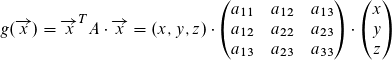
und rechnest es formal aus. Dann machst du einen Koeffizientenvergleich. D.h. du suchst x² und schaust welcher Koeffizient da stehen muß (5). Im formalen Produkt suchst du auch x² (a_11) und schließt a_11 = 5. Nun das gleiche mit y², z², xy und xz. Da kein yz-Term auftritt wird ein Element der Matrix gleich 0 sein.
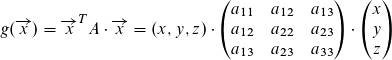
Ergänzung:
in der Aufgabenstellung muss nach dem und natürlich noch die Angabe zur Matrix "Q= x'Ax" stehen.
Die gesamte Aufgabenstellung ist also:
gegeben g(x)= 5x^2+3y^2+2z^2-xy+8xz und Q= x'Ax leiten Sie die symmetrische Matrix A her
Vielen Dank!
Wenn ich es richtig verstanden habe, kann ich so aus einer Gleichung mit 3 unterschiedlichen Variablen immer eine 3x3 Matrix ablesen, richtig? Also X^2 wäre immer q_11, y^2 immer a_22, xy = q_21/q_12 etc. und muss das, außer bei dieser Aufgabe in der ich es herleiten soll, nicht immer mühseelig ausrechnen. Liege ich damit richtig oder könnte x^2 bei den Variablen x, y und z auch eine andere Stelle als q_11 belegen?