Wie ist die Gravitationskraft zwischen Sonne und dem Planeten Jupiter?
Ich habe es einmal berechnet, habe ich die Aufgabe richtig berechnet? Es liegt mir nicht so besonders.
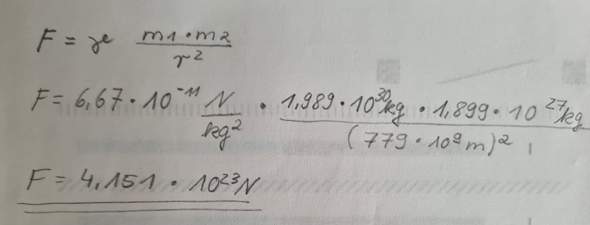
Über Rückmeldungen wäre ich dankbar.
3 Antworten
Die gravitative Kraft zwischen der Sonne und dem Planeten Jupiter kann mithilfe des Gravitationsgesetzes von Newton berechnet werden, welches besagt, dass die Kraft direkt proportional zum Produkt ihrer Massen und umgekehrt proportional zum Quadrat des Abstands zwischen ihren Zentren ist. Die Gleichung lautet wie folgt:
F = (G * m1 * m2) / r^2
Dabei:
F ist die gravitative Kraft zwischen den Objekten,
G ist die Gravitationskonstante (ungefähr 6,67430 × 10^-11 m^3 kg^-1 s^-2),
m1 ist die Masse des ersten Objekts,
m2 ist die Masse des zweiten Objekts, und
r ist der Abstand zwischen den Zentren der Objekte.
Um die gravitative Kraft zwischen der Sonne und Jupiter zu berechnen, benötigen wir die Masse der Sonne (m1), die Masse von Jupiter (m2) und den Abstand zwischen ihnen (r).
Die Masse der Sonne beträgt ungefähr 1,989 × 10^30 Kilogramm.
Die Masse von Jupiter beträgt ungefähr 1,898 × 10^27 Kilogramm.
Der durchschnittliche Abstand zwischen der Sonne und Jupiter beträgt ungefähr 778,5 Millionen Kilometer oder 7,785 × 10^11 Meter.
Indem wir diese Werte in die Gleichung einsetzen, erhalten wir:
F = (G * m1 * m2) / r^2
= (6,67430 × 10^-11 * 1,989 × 10^30 * 1,898 × 10^27) / (7,785 × 10^11)^2
Die Auswertung dieser Gleichung liefert uns die gravitative Kraft zwischen der Sonne und Jupiter.
Lesen Sie auch: Wie viele Jupiter passen in die Sonne? Enthüllung des erstaunlichen Maßstabs unseres Sonnensystems.
= (6,67430 × 10^-11 * 1,989 × 10^30 * 1,898 × 10^27) / (7,785 × 10^11)^2
Auch wenn es ungefähr das ist, was man in den Taschenrechner tippt: Die Einheiten wegzulassen, hat große Nachteile. Nicht nur, dass die Gleichung so gar keine physikalische Größe ergibt und mathematisch ohnehin falsch ist, sondern auch, dass man die Einheit des Resultats, statt sie zu errechnen, am Ende, nicht ohne Irrtumsrisiko, aus dem Nichts erzeugen muss, und es zudem sehr viel schwieriger wird, bei unplausiblen Ergebnissen nach der Stelle zu suchen, an der man sich vertan hat.
Ich empfehle darum, auch wenn es etwas länger wird, jede Größe vollständig hinzuschreiben:
(6.67430 * 10^-11 * N*m^2/kg^2 * 1.989 * 10^30 * kg * 1.898 * 10^27 * kg) / (7.785 * 10^11 * m)^2;
Die Einheit N ergibt sich dann beim Rechnen automatisch als Teil des Resultats.
Ob die Entfernung zwischen Jupiter und der Sonne und ihre Massen so richtig sind, kann ich nicht sagen, ohne es selbst nachschlagen zu müssen. Aber die Einheit der Gravitationskonstante ist falsch. Die ist nicht N/kg^2, sondern m^3/(kg * s^2), nur so kommt am Ende als Einheit für die Kraft N heraus.
So wie du es gemacht hast, bleibt N/m^2 übrig, weil sich alle kg gegenseitig wegkürzen und nur N über dem Bruchstrich und m^2 unter dem Bruchstrich stehen bleiben.
Für die Einheit der Gravitationskonstanten kann man gleich N*m^2/kg^2 schreiben. So ist auf einen Blick erkennbar, dass die Krafteinheit N herauskommt, wenn man zwei Massen damit malnimmt und durch das Quadrat ihrer Entfernung dividiert.
Nur eine Randbemerkung über richtiges Deutsch:
Über Rückmeldungen freut man sich, aber für Rückmeldungen ist man dankbar.