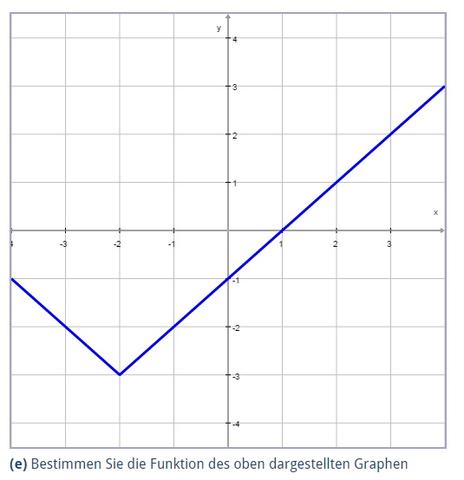
Wie ist der folgende Graph zu lösen? Wieso ist er V-förmig dargestellt? Ich komme auf f(x) = 0,5x2 + 2x - 1 was falsch ist?
5 Antworten
Wie würde ich die Funktion denn darstellen, wenn ich den Graphen nicht nach links, sondern nach rechts verschiebe?
Ich weiß nicht in welcher Klassenstufe Sie sind, aber verschieben nach rechts ist immer mit einem Minuszeichen.
Bsp:
1) x^2 ist die Normalparabel.
2) (x+2)^2 ist eine um 2 nach links verschobene Normalparabel.
3) (x-2)^2 ist eine um 2 nach rechts verschobene Normalparabel.
Die Normalparabel hat bei x = 0 ihren Scheitelpunkt mit f(0) = 0. Wenn ich oben in der zweiten Gleichung x = -2 einsetze erhalte ich den Wert 0. Bei der unteren Gleichung muß ich dafür x = +2 einsetzen, d.h. der Scheitelpunkt liegt nun nicht bei x = 0, sondern bei x = 2.
Ändere ich in der Funktion "x^2 + 2x" das x zu (x-2), erhalte ich die Funktion: "(x-2)^2 +2*(x-2)".
Sie hat die gleiche Form wie die erste Funktion ist aber um zwei nach rechts verschoben.
Genau dasgleiche gilt für den Betrag auch: |x+2| nach links und |x-2| nach rechts.
das ist keine quadratische, sondern eine lineare Funktion - und zwar eine mit einem Betrag drin (also grob in der Form f(x) = Betrag von (x + Zahl1) + Zahl2)
schau dir den Graphen von |x| (Betrag x) an.
dein graph ist nur noch etwas verschoben.<
Frag nochmal wenn es dir nicht weiterhilft
Ja, genau!
Ich habe bis jetzt noch nie mit Beträgen gearbeitet, wenn es um Funktionen ging :S
F(x)=mx+b ist die Form die ich kenne.
Das wäre ja dann
F(x)=|x+2|-3
Wie würde ich die Funktion denn darstellen, wenn ich den Graphen nicht nach links, sondern nach rechts verschiebe?
Leider verstehe ich es noch nicht so ganz, eine solche Aufgabe bearbeite ich zum ersten Mal.
Um die Aufgabe zu lösen, müsste ich mir noch ein wenig mehr Grundwissen aneignen.
die funktion y(x) = x ist ja eine schräger linie durch den Usprung mit steigung 1 (Winkel45°).
die funktion y(x) = |x| unterscheidet sich nur insofern als das jedes X positiv gewertet wird. die funktion hat bei x= -1 ja per definition den y-wert |-1| also 1. Daher geht der Graph im negativen Bereich nicht nach links unten sondern nach links oben.
y = |x + 2| - 3
eine solche antwort hilft nicht wirklich wenn anscheinend noch nichtmal klar ist was |x| bezeichnet
Eine möglichst minimale Beschreibung der zugrunde liegenden Funktion wäre x |—> |x|, nur horizontal (um –2) und vertikal verschoben (um –3). Daher ist die Funktion der Form: ƒ : x |—> |x– -2| + -3 = |x+2| – 3.
also deine aufgabe ist doch die funktion y(x) zu finden die deinen graphen dartsellt oder?