Wie geht die Ableitung von ln Funktion?
Leute wie leite ich das ab? Habe distanzunterricht und mein Lehrer muss erstmal meine anderen E-Mails beantworten. Wie geht das?
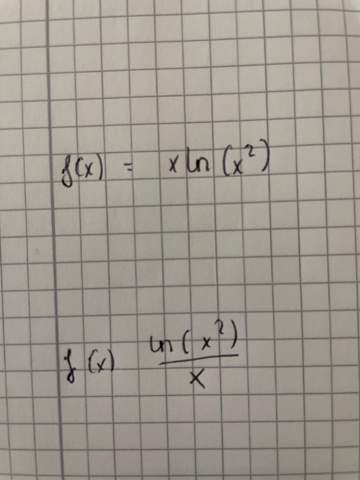
Ich benötige die Ableitung. Wäre schon wenn eine leichte kurze verständnisvolle Erklärung dabei wäre.
Und Was passiert mit dem x vor ln?
2 Antworten
Die Ableitung von ln(x) ist 1/x, Um die Ableitung der Funktion f(x) = x * ln(x^2) zu berechnen formst du erst mal um. f(x) = x * ln(x^2) = 2 * x * ln(x) und jetzt kannst du die Produktformel verwenden. f(x) = u(x) * v(x) mit u(x) = 2*x und v(x) = ln(x) =>
f´(x) = u´(x) * v(x) + u(x) * v´(x) .
Nachtrag auf Grund der Nachfrage:
Ich verstehe die Umformung nicht. Warum landet die 2 nach vorne ?
Diese Rechenregel sollte man gelernt haben.
Zur Erläuterung: lg(100) = 2 =lg(10^2) = 2 * lg(10) ;
Ich werde noch meine Antwort um die Herleitung der entsprechenden Zusammenhänge ergänzen.
Das erste ist ein Produkt, dazu benötigst du die Produktregel, das zweite ein Quotient, dazu benötigst du die Quotientenregel.
Ja willst du das hier vielleicht vorgerechnet haben zum Aufgabenabschreiben?
Dankeschön.Warum wird aber aus ln(x^2) 2* x*ln(x)? Kann ich nicht 2*x +x*ln machen? Warum und wie verschwindet das x vor ln?