Wie bestimmt man Potenzfunktionen mit negativen/positiven Exponenten?
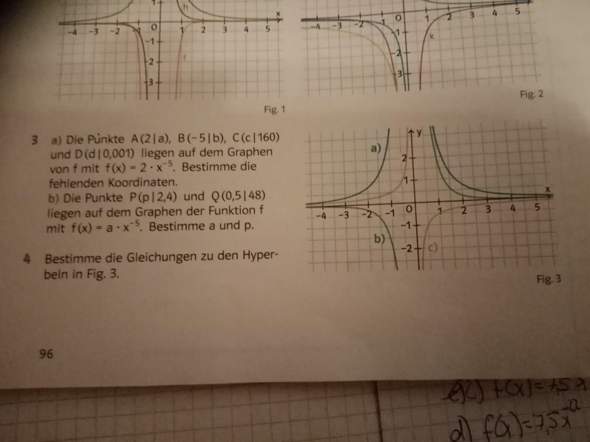
Hallo verstehe dieses Thema nicht, brauche dringend Hilfe. Wann die Exponenten ungerade sind oder gerade weiß ich, kapiere aber nicht wie man dann die gesamte Funktion rauskriegt (Steigung, Exponent...) . Kann mir jemand anhand der Aufgabe (Nr. 4) erklären wie das geht. Danke im voraus
2 Antworten
Ihr seid ja offensichtlich noch bei der einfachsten Form von Potenzfunktionen mit negativen Exponenten, die nicht verschoben sind und nur ganzzahlige Exponenten haben.
Deren Grundform lautet:
f(x) = a * x^-n
1) Bestimmung von a.
Dabei machen wir uns zunutze, dass 1 hoch irgendwas immer 1 ergibt. Dadurch gitl:
f(1) = a * 1 = a
Wir lesen also den Funktionswert (y-Wert) bei x = 1 ab und das ist dann auch schon a:
a) f(1) = 3
a = 3
b) f(1) = 2
a = 2
Tipp: da man bei +1 nicht klar erkennen kann, was a) und b) ist, kann man den Betrag auch bei -1 ablesen, die Kurven sind ja immer symetrisch, entweder zur x-Achse (gerade Exponenten) oder zum Ursprung (ungerade Exponenten)
c) f(1) = -0,5
a = -0,5
Jetzt müssen wir noch den Exponenten rauskriegen. Dazu dient uns der Funktionswert bei -2.
Zuerst formen wir aber noch um:
aus f(x) = a * x^-n folgt:
x^-n = f(x) /a
a) f(-2) = 0,75
-2^-n = 0,75 /3 = 0,25 = 1/4
1/-2^-n = 1/4
-2^n = 4
n = 2
damit lautet a):
f(x) = 3x^-2
b) f(-2) = -0,25
-2^-n = -0,25/2 = -0,125 = -1/8
-2^n = -8
n = -3
Damit lautet b):
f(x) = 2x^-3
c) f(-2) = 0,25
-2^-n = 0,25/-0,5 = -0,5 = -1/2
-2^n = -2
n = 1
damit lautet c):
f(x) = -0,5x^-1
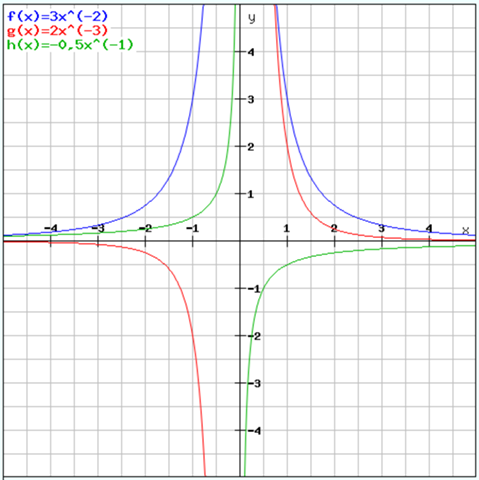
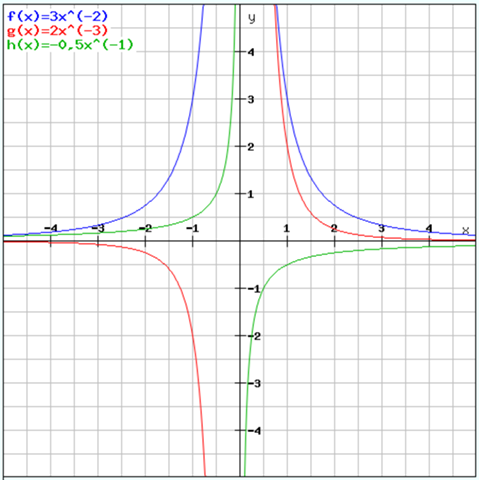
Der Funktionsplotter sagt, das stimmt:
Danke für die Antwort aber wieso kann von - -2^-n=1/4 zu-2^-n=4
Durch Kehrwertbildung
-2^-n = 1/-2^n = 1/4
Aus 1/-2^n = 1/4 wird dann als Kehrwert:
-2^n = 4
Da man ja die Potenzen von 2 kennt, muss man auch nicht mit einem Logarithmus weiterrechnen, sondern kann das Ergebnis sofort sehen. Man muss allerdings beim Vorzeichen von n tierisch aufpassen....da sind mir in der Antwort einige Fehler reingerutscht.
Und wie kommt man auf 1/2 weil 0,25 ist ja schon ein Viertel wieso teilt man dann auch 1 durch 2
meinst du bei c)?
f(-2) = 0,25 (abgelesen)
a = -0,5 (oben berechnet)
Damit ergibt f(x) /a:
0,25 /-0,5 = -1/2
also ist:
-2^-n = -1/2
Kehrwert:
-2^n = -2
n = 1
Schon ok, Hauptsache am Ende hast du es begriffen und schreibst eine gute Note.
Ne meinte -1/2
Das Minus vor dem 1/2 kommt durch a = - 0,5 da rein
Und warum teilt man dann 1/2^-n
Das ist ein Schreibfehler:
-2^-n = 1/-2^n und nicht 1/-2^-n
a) muss einen geradzahligen Exponenten haben. Man setze an:
- y = a * x^(-b)
a ist ein Parameter. Zur Funktion gehört der Punkt A(1/3), deswegen:
- 3 = a * 1^(-b) = a
- y = 3*x^(-b)
Man probiere b durch für 2, 4, 6,..., vergleiche die Graphen und man sieht, dass b=2 am nächsten der Abbildung kommt. Analog macht man das bei den anderen Funktionen.
b) A(1/2) ist Punkt der Funktion. Damit ist
- 2 = a * 1^(-b) = a
b probiert man durch für b=1, 3, 5... und man sieht, dass b=3 am besten passt.
c) A(1/-0,5) ist Punkt der Funktion. Sie hat offenbar einen ungeradzahligen Exponenten und ein negatives Vorzeichen. Ansatz:
- y = - a * x^(-b)
- -0,5 = - a * 1^(-b)
- a = 0,5
b=3 passt am besten.
Korrektur:
Habe oben geschrieben bei b):
n = -3
Muss heißen:
n = 3
Und statt 1/-2^-n = 1/4
müsste es heißen:
-2^-n = 1/4
...ist halt schon spät...