Wie berechnet man den Schwerpunkt von halbem Kreissegment?
Hallo Community,
zur Berechnung einer Aufgabe muss ich eine Schwerpunktberechnung durchführen. Es handelt sich dabei um den Schwerpunkt eines halben Kreissegments, d.h. halbiert an der Symmetrielinie.
Habt ihr einen Ansatz für mich? Vielen Dank schon im voraus!
AndrijaG
3 Antworten
So könnte es gehen:
Der Schwerpunkt einer aus zwei Teilen zusammengesetzten Figur liegt auf der Geraden durch die Schwerpunkte beider Teile.
Mit folgenden Konstruktionen kannst Du (redundant) 3 Geraden bestimmen, die den gesuchten Schwerpunkt S=(sx; sy) enthalten:
- Spiegle die blaue Figur an der y-Achse. Den Schwerpunkt A=(0;ay) des entstandenen Kreisabschnitts kann man berechnen. Aus Symmetriegründen gilt sy=ay.
- Erweitere die blaue Figur zu einem Kreisausschnitt. Dessen Schwerpunkt B sowie den Schwerpunkt D der hinzugefügten Dreiecks kann man berechnen.
- Die blaue Figur lässt sich in einen Kreisabschnitt mit Schwerpunkt U und ein Dreieck mit Schwerpunkt T zerlegen. Für beide Punkte gibt es Formeln.
Der Rest ist Hausaufgabe: Bestimme die Gerade BD (oder TU) und finde darauf den Punkt mit der Abszisse ay.
P.S.: Schon die Formeln für Kreisausschnitt und Kreisabschnitt sind ja "nicht ohne". Ich befürchte, dass die Formel für S so richtig schön hässlich wird. Daher würde ich wohl BD und TU ermitteln und hoffen, dass beide Wege zum selben Ergebnis führen.
Du kannst Deinen Rechenweg gern hier präsentieren — vielleicht findet jemand ja doch noch einen Vorzeichen- oder Klammerfehler drin.
Viel Spaß!
Danke schonmal. Der Ansatz könnte stimmen. Sobald ich die Lösung habe werde ich sie hier veröffentlichen. Mit Rechenweg wenn möglich ;)
Meinst du jetzt einen Halbkreis-ring oder schon die Fläche? dafür gibt es ja unterschiedliche Formeln!
z.B. siehe Seite 3 http://www.wolfgang-gerhards.de/zip/schwerpunkt.pdf
und hier gibt es eine schöne Tabelle, sehr zum empfehlen und gehört in deine FS ;)
goessner.net/download/learn/tm/statik/Statikformeln.pdf
Die Seite habe ich auch gefunden ^^ Was ich meine ist jedoch ein halbes Kreissegment. Auf Seite 3 bei Kreissegment sozusagen der Schnitt mit einer Geraden durch M und S. Der Schwerpunkt von einer Hälfte verschiebt sich von S dann nur noch nach rechts bzw. links. Beide Hälften zusammen heben sich auf, weswegen S bei "0" liegt. Ich brauche jedoch nur eine Hälfte also auch den senkrechten Teil.
4 r
= - * ----
3 Pi
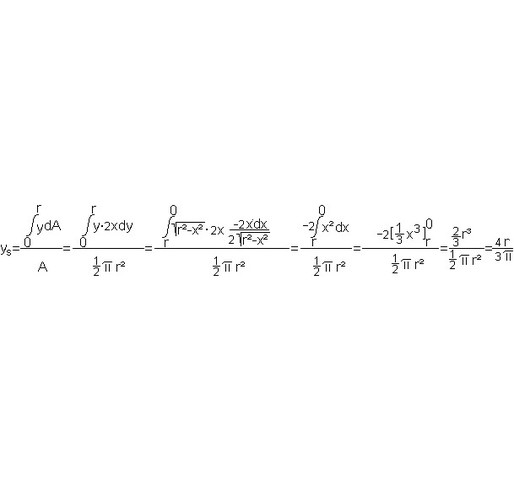

Danke dir! Woher hast du denn die Lösung?