Welche gewürfelte Summe ist durchschnittlich höher?
Hallo zusammen. Ich hätte eine Frage. Bei welchem Szenario ist der gewürfelte Wert/Summe im Durchschnitt höher?
Szenario A)
2 Würfel (sechsseitig). Beide werden gewürfelt und beide Ergebnisse summiert.
Szenario B)
2 Würfel (zwölfseitig). Beide werden gewürfelt, jedoch wird nur das höhere Ergebnis gewertet.
Lieben Dank schonmal.
5 Antworten
(A) ist, wie schon andere gesagt haben, der doppelte Erwartungswert eines Wurfs, also gleich 7.
(B) Es gibt 12 * 12 = 144 mögliche Ausgänge, der Erwartungswert ist gleich
Summe( i= 1; 12; Summe( j= 1; 12; Max{i; j} ) ) / 144 = 8.46....
Man kann sich die Summe in einem Rechner addieren lassen oder (für allgemeines n) formelmässig auflösen,
Summe( i= 1; n; Summe( j= 1; n; Max{i; j} ) ) =
Summe( i= 1; n; Summe( j= 1; i; i ) ) + Summe( i= 1; n; Summe( j= i+1; 12; j ) ) =
Summe( i= 1; n; i^2 ) + Summe( i= 1; n; n(n+1)/2 - (j+1)(j+2)/2 ) =
.... =
n(4 n^2 + 3 n -1)/6
Hallo.
Vorteil der Summe liegt darin, dass du mindestens die Augenzahl 2 bekommst. Beim zwölfseitigen Würfel besteht immerhin noch die Chance von 1/144, dass es eine 1 wird.
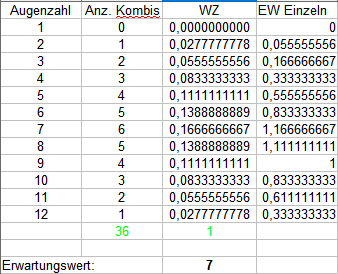
Summe zwei 6-seitiger Würfel:
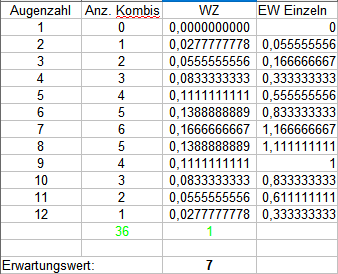
Zwei 12-seitige Würfel:
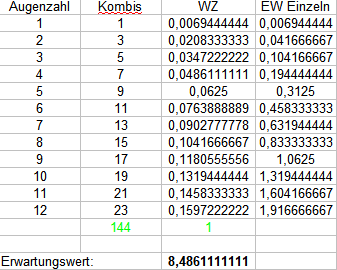
Ich hoffe, das beantwortet deine Frage ausführlich genug, wobei ich keine Garantie auf Richtigkeit übernehme. Ich bin nicht ausgeschlafen. 😮😉
LG
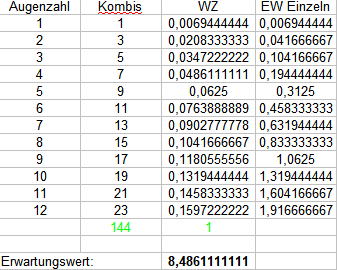
Vielen dank für die ausführliche Antwort, die Tabelle ist äußerst hilfreich. :)
Die Rechnung ist ziemlich kompliziert. Der durchschnittliche Wert eines 6seitigen Würfels beträgt 3,5. Addierst du die zwei Würfel also 7. Der Durchschnitt eines 12seitigen Würfels ist 6,5. Da du aber immer den höheren der beiden Würfel wertest, kann man hier nicht mit dem Durchschnitt arbeiten. Und an diesem Punkt ist leider mein Wissen in Stochastik erschöpft, da zu lange her. Ich hoffe du findest hier einen Experten 😉
Szenario 1 ergibt im Durchschnitt (1 + 6 oder 2+5 ...) = 7
Szenario 2 ergibt mindestens 6,5 ((1 + 12)÷2)
Da aber zu 25% ein Würfel die kleinere Zahl (3,5) hat, 50% gleich (6,5), 25% eine größere Zahl (9,5) und du die kleinere wegläßt, bleiben (6,5 + 6,5 + 9,5)÷3 übrig, das ergibt dann 7,5 im Durchschnitt
Szenario B hätte dann den höheren Durchschnitt
(Der Rechenweg kann falsch sein, aber die Richtung stimmt hoffentlich.)
Ich würde den Durchschnitt sogar mindestens auf 27 bis 30% oder höher über die durchschnittlichen 6,5 festlegen. Also mind 8,1 oder mehr.
"Würde das fehlen der 1 nicht zu einem höheren Durchschnitt führen?"
Ja. tut es. Der Durchschnitt ist bei den addierten Würfeln ja gleich 7, beim Durchschnitt des 12er Würfels gleich 6,5.
Tipp: Der Erwartungswert bei so einem Würfel mit n-gleichen Seiten und entsprechender Augenzahl von 1 bis n ist immer:
Und da kommt dann 7/2 für einen 6-seitigen Würfel raus und 13/2 für einen 12-seitigen Würfel
Danke für die Erklärung. Das macht mir größtenteils Sinn. Bei Szenario A könnte man ja nur die Summe von 2-12 erwürfeln. Würde das fehlen der 1 nicht zu einem höheren Durchschnitt führen?