Was ist der Unterschied zwischen Wendepunkt und Terassenpunkt?
5 Antworten
Stell dir vor, Du fährst mit dem Auto eine Kurve/Funktion entlang. Ein Wendepunkt ist dort, wo eine Linkskurve in eine Rechtskurve (oder umgekehrt) übergeht, in einem Terrassenpunkt ist zwar auch die Steigung Null, aber man bleibt quasi in der Links- ( bzw. Rechts-)kurve, auch wenn man für einen kurzen Augenblick geradeaus fährt.
Stimmt, habe mich vertan. Aber die Links-/Rechtskurve bezieht sich auf die Ausgangsfunktion (wenn man da mit "Auto" entlangfährt, kann man von Links- und Rechtskurve sprechen., ja nachdem, ob man das Steuerrad nach links oder rechts drehen muss).
Ja genau, das bezieht sich auf die Ausgangsfunktion. Man hat aber je nach Krümmung (zweite Ableitung) gerade eine Links- oder eine Rechtskurve in der Ausgangsfunktion.
In einem Wendepunkt ändert sich das Krümmungsverhalten eines Graphen (daher der Name!).
Ein Sattelpunkt ist ein spezieller Wendepunkt, nämlich ein WP mit waagerechter Tangente (Steigung 0).
siehe Bild
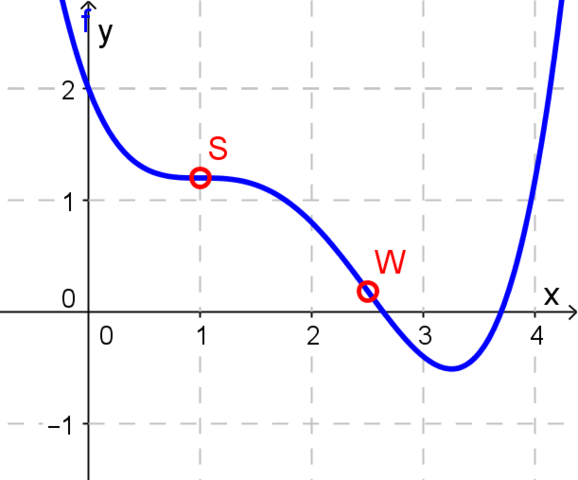
Einen "Sattelpunkt" bezeichnet man auch als "Terrassenpunkt".
Der "Sattelpunkt" ist ein spezieller Wendepunkt,bei dem die Tangente waagerecht zur x- Achse liegt.
Bedingung Wendepunkt f´´(x)=0 und f´´´(x) ungleich Null
" "Sattelpunkt (Terrassenpunkt) f´´(x)=0 und f´´´(x) ungleich Null
außerdem noch f´(xw)=0 weil ja hier die Tangente im Wendepunkt waaagerecht zur x-Achse liegt.
Bedingung Wendepunkt f´´(x)=0 und f´´´(x) ungleich Null
Der zweite Teil ist nicht korrekt; f´´´(x) ≠ 0 ist keine (notwendige) Bedingung für eine Wendestelle, vgl. f(x) = x^5.
steht so in meinen Mathe-Formelbuch
Wendepunkt f´´(xw)=0 und f´´´(xw) ungleich Null
Sattelpunkt=Stufenpunkt=Terrassenpunkt
sind auch f³(xw)=0 .....f⁽k-1)=0 aber f^(k)(xw) ungleich 0 ,liegt für k=ungerade auch ein Wendepunkt vor
Da steht allerdings "hinreichende Bedingung", d.h. WENN diese Bedingung erfüllt ist, liegt auf jeden Fall eine Wendestelle vor.
Das heißt aber nicht, dass diese Bedingung unbedingt erfüllt sein muss, damit es zu einer Wendestelle kommt.
Deshalb gibt es ja auch noch das (in der Schule nicht ganz so übliche) Kriterium des Vorzeichenwechsels der 2. Ableitung. Diese Bedingung ist sowohl notwendig als auch hinreichend, klappt also immer! (Und hat noch den Vorteil, dass man die 3. Ableitung nicht zu bilden braucht; das kann ja ganz schön Arbeit sein.)
(Nur so zur Klarstellung für den Fragesteller :-) )
Man kann aber auch noch die Krümmung berechnen,vor xw und nach xw.
Ein Wendepunkt teilt 2 Kurvenbögen (konvex und konkav),siehe Mathe-Formelbuch "Differentialgeometrie"
Terassenpunkt = Sattelpunkt
Ein Sattelpunkt ist ein Wendepunkt, bei dem zusätzlich f´(x_w) = 0 ist, also ein Wendepunkt mit horizontaler Tangente, die die Steigung Null hat.
Wobei x_w die Stelle x ist, an der der Wendepunkt entlang der x-Achse liegt.
Normaler Wendepunkt :
f´´(x_w) = 0
f´´´(x_w) ≠ 0
Sattelpunkt / Terassenpunkt :
f´(x_w) = 0
f´´(x_w) = 0
f´´´(x_w) ≠ 0
Es gibt noch eine strengere Definition für einen Wendepunkt, der jedoch in der normalen Schule für gewöhnlich keine Rolle spielt. Dazu schaue mal im "Schülerduden: Die Mathematik Band 2" unter dem Thema "Wendepunkt".
Auf Wikipedia findet man die strengere Definition auch :
https://de.wikipedia.org/wiki/Wendepunkt
Schaue mal unter "Hinreichendes Kriterium unter Verwendung weiterer Ableitungen"
im Terassenpunkt ist die Steigung 0.
Und sonst ist es halt ein Wendepunkt.
Das stimmt so nicht. Dieses Linkskurve/Rechtskurve bezieht sich nicht auf die Steigung, sondern auf die Krümmung (zweite Ableitung). Bei einem Wendepunkt ist die Krümmung null. Bei einem Sattel- bzw. Terrassenpunkt ist nun zusätzlich die Steigung null. Deswegen wird aus einer Links- trotzdem eine Rechtskurve (oder umgekehrt). Der Terrassenpunkt ist also ein Spezialfall des Wendepunkts, bei dem zusätzlich noch die Steigung gleich Null ist. Das ist nicht zwingend bei einem Wendepunkt der Fall.
Für den Fragesteller:
https://de.serlo.org/mathe/funktionen/kurvendiskussion/kruemmungsverhalten-wendepunkte/wendepunkt-terrassenpunkt