Was genau ist ein Wort bei einem Alphabet (Mathematik / Informatik)?
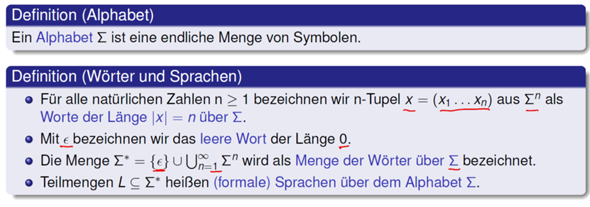
Was mich verwirrt, also wir haben stehen, dass wir ein n-Tupel aus Σ haben! Nun verstehe ich das ganze nicht, wue bilden wir das Wort? Es ist ja keine Teilmenge von Σ, ist es dann so, dass wir das karthesische Produkt bilden? Also z. B.
ΣxΣxΣ würde Wörter der Länge 3 entstehen lassen? Meint man das mit n Tupel?
4 Antworten
Ein n-Tupel ist ja nichts anderes als eine geordnete Folge von n Elementen (Reihenfolge ist essentiell). Das kartsische Produkt Sigma^n spannt im Endeffekt die Menge aller möglichen Tupel der Länge n auf, was letztlich dem karteischen Produkt und somit allen Wörtern der Länge n entspricht. (Jede Komponente des Tupels ist ein Element der Menge Sigma)
Ob ich ein Tupel nun formal in einer vektorähnlichen Notation niederschreibe, oder wie in der Programmierpraxis als Zeichenkette spielt keine essentielle Rolle.
Was dem Programmierer der Zeichensatz, ist in der theoretischen Informatik das Alphabet (Symbolvorrat), was in der theoretischen Informatik das Wort, ist in der Programmierpraxis die Zeichenkette.
Das, was man auch umgangssprachlich darunter versteht:
eine (theoretisch beliebig lange) Folge von Buchstaben aus dem Alphabet.
Teilmengen von "Sigma-Stern" sind dann die in der jeweiligen Sprache sinnvollen Wörter
Ich würde es ohne Komma schreiben. Σ² = { aa, ab, ba, bb }. Also die Menge aller Wörter der Länge 2. Σ* sind alle Wörter beliebiger Länge einschl. des leeren Worts
Ein Tupel x ist ein Wort, wenn es aus Wörtern der Menge Σ besteht.
Die Menge Σ* ist definiert als eine Vereinigung von Epsilon (leeres Wort) und der Vereinigung der Mengen Σ^n wobei n=1 BIS unendlich ist. Ich denke, du hast das Unendlichkeitszeichen übersehen.
Das heißt also Σ* beinhaltet {Epsilon},{1},{2} usw.
Ein Wort der Länge |3| = n ist Teil einer Menge Σ^3, also z.B. {{1},{2},{3}}. Deine Aussage mit ΣxΣxΣ sollte auch korrekt sein.
Ich verweise einfach mal dreist auf eine andere Antwort von mir:
Um deine Frage zu beantworten: Ein n-Tupel über Σ ist nichts anderes als ein Element von Σ^n.
Genau, aber ist Σ^n das kartesische Produkt? Beispiel Σ={a,b}
Σ^2 =ΣxΣ={(a,b),(a,a),(b,a),(b,b)}
Könnte man nun sagen, dass ein Wort z. B. das ist? also (a,b)?
Ja, (a,b) wäre ein Wort der Länge 2 über Σ.
Später wirst du das nicht mehr als "(a,b)" schreiben sondern nur als "ab", sodass der Begriff Wort ein wenig intuitiver erscheint.
Okay danke, also ist es eigentlich das kartesische Produkt immer, was mir die möglichkeiten aller Wörter der länge 2 gibt, in dem Beispiel, wenn ich das 2x verknüpfe! Danke dir! Aber was unterscheidet nun Σ^n von Σ*? Also ist das nicht gleich?
Ach Σ^n hat immer eine festgelegte Anzahl an Wörtern, z. B. Σ^2 wären alle Wörter mit 2 Buchstaben, wohingegen Σ* alle möglichen Wörter hat oder? Und zählen eigentlich auch einzelne buchstaben als Wörter, wenn man z. B. Σ^1 macht?
Σ^n ist eben die Menge aller Wörter der Länge n. Wie du eben festgestellt hast, besteht Σ^2 aus den 4 Wörtern aa, ab, ba und bb. Σ^1 besteht aus den Wörtern a und b.
Σ* hingegen besteht aus allen Wörtern. D.h. Darin liegen sowohl die Wörter der Länge 1, die Wörter der Länge 2 usw.
Genau, aber ist Σ^n das kartesische Produkt? Beispiel Σ={a,b}
Σ^2 =ΣxΣ={(a,b),(a,a),(b,a),(b,b)}
Könnte man nun sagen, dass ein Wort z. B. das ist? also (a,b)?