Warum schwingt der Körper K harmonisch?
Ein Körper hat die Masse m und ist zwischen zwei gleich-gedehnten Federn eingespannt. Sowohl die rechte, als auch die linke Feder haben die Federkonstante D.
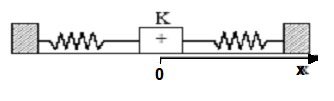
Aus der Ruhelage 0 wird der Körper nach rechts um x ausgelenkt und zu t=0s freigegeben.
Warum schwingt der Körper harmonisch?
3 Antworten
Bedingung für eine harmonische Schwingung, ist dass die Rückstellkraft direkt proportional zu der Auslenkung ist. Wenn man nun also das Objekt verschiebt, so zieht einerseits die eine Feder mit einer Kraft F_1=D*(s'+s) (mit s' die ursprüngliche Auslenkung bei Ruhelage vom Objekt) und die andere Feder mit F_2 = D*(s'-s)
Das ergibt eine gesamte Kraft von F = F_1 - F_2 = D*(s'+s) - D*(s'-s) = D*((s'+s)-(s'-s)) = 2*D*s
(unter der Annahme, dass keine weiteren Kräfte wie z.B. Reibung wirken)
Damit ist die Kraft direkt proportional zu der variablen Auslenkung. Das war zu zeigen.
Sofern keine Reibung oder sonstige Effekte vorliegen, kannst du ganz normal davon ausgehen, dass die Rückstellkraft die ist, die ich oben angegeben habe und die Amplitude konstant bleibt, da keine Energie verloren geht.
Die Auslenkung ist nicht gegeben in der Aufgabenstellung. Ist es dann überhaupt möglich die Frequenz/Amplitude zu berechnen?
Du hast ja aber die Geschwindigkeit in der Gleichgewichtslage gegeben. Damit kannst du z.B. über Energieerhaltung (Spannenergie in kinetische Energie) die ursprüngliche Auslenkung ausrechnen. Für die Frequenz brauchst du nur die normale Formel für Federpendelfrequenzen zu verwenden, wobei die Federkonstante in diesem Fall dann 2*D ist.
Also 1/2*(2D)s^2=1/2*mv^2 <=> Ds^2=1/2*m*v^2 => s^2=(mv^2)/(2D)?
Exaktamente! Und da wie gesagt die Auslenkung gleich bleibt, da keine Verluste vorhanden sind, ist dies zugleich die Amplitude.
Dachte ich mir schon, vielen Dank für die Hilfe. Die Frequenz erhalte ich dann einfach über T=2pi*sqrt(m/(2D)) und dann f=1/T
Warum kann man eigentlich den Energieerhaltungssatz anwenden? Ist nicht in der Ruhelage die Geschwindigkeit am höchsten und damit die kinetische Energie maximal und die Spannenergie minimal, d. h. 0?
Jap! genau deswegen geht das so! Energie bleibt erhalten. Also:
E_kin+E_spann=E_kin'+E_spann' (gestrichene Größen sind die in der Ruhelage, die anderen die am maximalen Auslenkpunkt)
Da bei der maximalen Auslenkung die kinethische Energie 0 ist, fällt also E_kin weg. In der Ruhelage ist die Spannenergie E_spann' 0, da die Feder relativ zum Anfang nicht weiter getreckt wird.
Das vereinfacht sich zu:
0 + E_spann = E_kin' + 0
=> E_spann = E_kin'
Wenn ich also frage, wann Spann- und kinetische Energie erstmals gleich sind, wähle ich 1/2(2D)s^2=1/2mv^2 an?
Wie bereits gesagt, lautet die komplett richtige Darstellung der Energie zu jeder Zeit:
E = E_kin+E_spann
Wenn du dir jetzt die Spannenergie am maximalen Auslenkpunkt anschaust, dann ist dies zu diesem Zeitpunkt die gesamte Energie, da dort weder kinetische noch sonstige Energien auftreten (mit Annahme keine Reibung etc.).
In der Ruhelage, wird dies ebenfalls mit der kinetischen Energie durchgeführt. Hier ist die Spannenergie Null, weswegen die kinetische Energie die Gesamtenergie darstellt.
Bezeichnet man mit s=0 die Ruhelage und s=s_max die höchste Auslenkung, dann gilt also:
E = E_kin(0) = E_spann(s_max)
Gleichheit gilt also nur in diesen speziellen Punkten.
Wenn du wirklich wissen möchtest, wann beide Energien Gleichzeitig oder am selben Punkt gleich sind, musst du zunächst davon ausgehen, dass sie am gleichen Punkt (dies sei mal s=s') gleich sind, also:
E = E_spann + E_kin = 2*E'
=> 2*E' = E
=> E' = E/2 = E_spann(s_max)/2 = E_kin(0)/2 = E_spann(s') = E_kin(s')
Dann kannst du dir darüber ausrechnen, bei welcher Ausrenkung beide Energien gleich sind, aber das wird komplizierter.
Ah, perfekt. Das ist dann wohl ein "formalerer" Beweis und vermutlich eher gefragt, als eine mündliche Erläuterung. Danke.

Gruß, H.

Hallo, könntest du mir vielleicht bei einer Aufgabe zum Federpendel helfen die sieht etwas kompliziert aus
@Halswirbelstrom
Weil bei einer Feder die Rückstellkraft proportional zur Auslenkung ist und beide Federn gleich sind
Nehmen wir mal an der Körper hat m=0.5kg Masse, die Federkonstante sei D=10 N/m. Wir lenken den Körper wieder nach rechts um x aus bei t=0s. Beim Durchgang der Gleichgewichtslage, hat der Körper eine Geschwindigkeit von v=0.63 m/s.
Muss ich bei diesem Feder-Masse-System irgendwas beachten, wenn ich die Frequenz und die Amplitude der Schwingung berechnen möchte?