Vektorraum, Abstand, Norm mit Polynom?
Hi,
komme hier nicht weiter, da die Tutorin nur die Lösung mitgeteilt hat, aber ohne Rechenweg:
Man betrachte den Vektorraum der Polynome von Höchstgrad 1 mit dem inneren Produkt
⟨f, g⟩ = ∫(1−1) f(x)g(x)dx
und darin die Polynome p1=2x und p2 =-1/3. Berechne den basierenden Abstand d(p1,p2)
Die Lösung ist:
Ich weiß nicht, wie man auf diese Lösung kommt. Und google rettet mich nicht wirklich, da ich eine Beispielrechnung dafür brauche.
Mein Ansatz war:
(p1,p2) = sqrt (2x+1/3)^2, aber die Lösung haut nicht hin.
danke!!!
2 Antworten
Ich weiß nicht genau, wie du zu deinem Ansatz „(p1,p2) = sqrt (2x+1/3)^2“ gelangt bist. Vielleicht hast du da in Richtung euklidischer Norm gedacht? Wofür du dann aber eher „sqrt((2x)² + (1/3)²)“ statt „sqrt((2x)² + (1/3)²)“ rechnen müsstest, was aber hier auch nicht richtig wäre.
Wenn man ein inneres Produkt (auch Skalarprodukt genannt) gegeben hat, so erhält man für die dadurch induzierte Norm mittels...
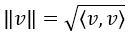
Und damit dann weiter die dadurch induzierte Metrik mittels...
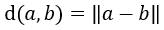
D.h. für alle a, b im Vektorraum ist dann...
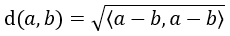
============
Im konkreten Fall...
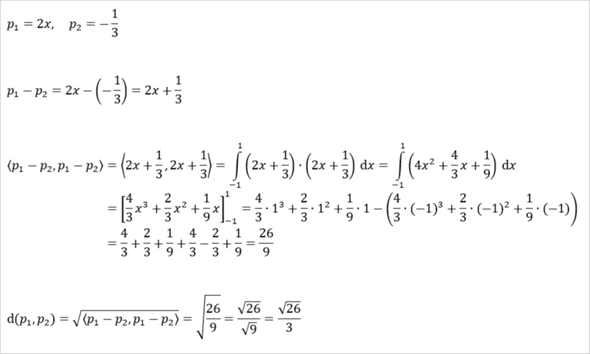
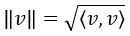
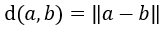
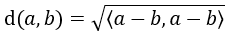
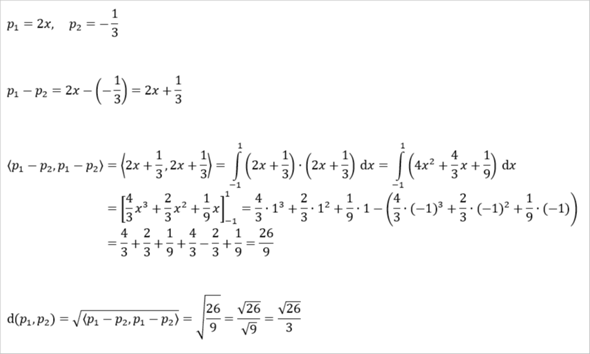
Also es gilt ja d(p,q)=sqr(<p-q,p-q>)
p1(x)-p2(x)=2x+1/3
Das quadriert ergibt
4x^2+4/3x+1/9
Dessen Stammfunktion ist
4/3x^3+2/3x^2+1/9x
Wenn man nun die Integralgrenzen (1 und -1) einsetzt erhält man somit:
4/3+2/3+1/9-(-4/3+2/3-1/9)=8/3+2/9=24/9+2/9=26/9
Und wenn du davon die Wurzel ziehst erhälst du sqr(26)/3
Somit ist d(p1,p2)=sqr(26)/3