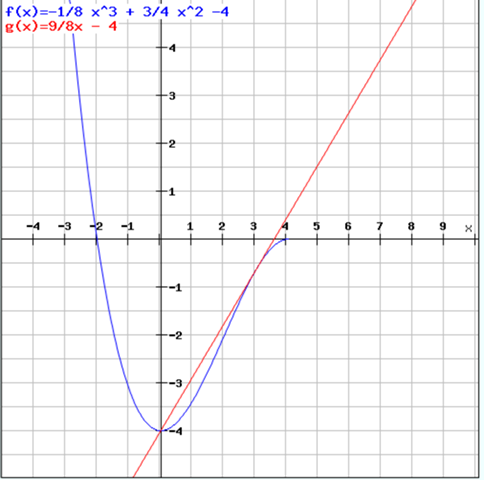
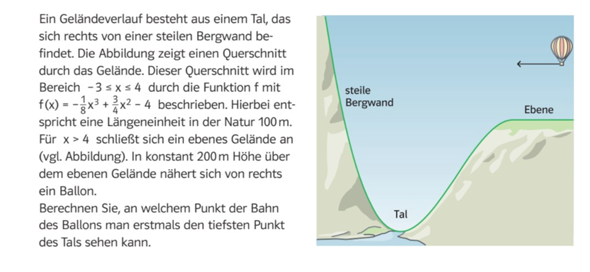
Tangenten und Normalen Aufgabe?
Hey, wir müssen in Mathe eine Aufgabe machen, aber ich verstehe nicht, wie ich hier vorgehen muss. Ich hab die erste Ableitung gebildet, aber weiß nicht, wie ich weiter machen muss.
2 Antworten
Es müsste der Punkt sein, wo die Tangente der Wendestelle die Flugbahn des Ballons schneidet, wenn ich mich nicht irre.
Dafür musst du die Wendestelle ausfindig machen (f"(x)=0) und dafür die Tangente bilden und diese mit ?g (x)=2? für den Ballon gleichsetzen.
Entscheidend ist die sogenannte Sichtlinie rauszukriegen.
Das ist eine Gerade
g(x) = ax - 4 mit a ≻ 0
Nun gibt es zwei Bedingungen:
Beide müssen einen gemeinsamen Berührpunkt haben:
g(xb) = f(xb)
a xb - 4 = - 1/8 xb^3 + 3/4 xb^2 - 4 (Gl.1)
Außerdem muss die Steigung im Punkt xb = a sein:
Dazu müssen wir die Ableitung von f(x) bilden:
f'(x) = -3/8 x^2 + 3/2 x
und dadurch ergibt sich:
a = -3/8 x^2 + 3/2 x
Das setzen wir in Gl.1 ein und erhalten:
-1/4 xb^3 + 3/4 xb^2 = 0
Dafür erhalten wir als Lösungen 0 und 9/8. Da a ≻ 0, bleibt nur a = 9/8 übrig. Damit haben wir:
g(x) = 9/8 x - 4
Das sieht dann so aus:
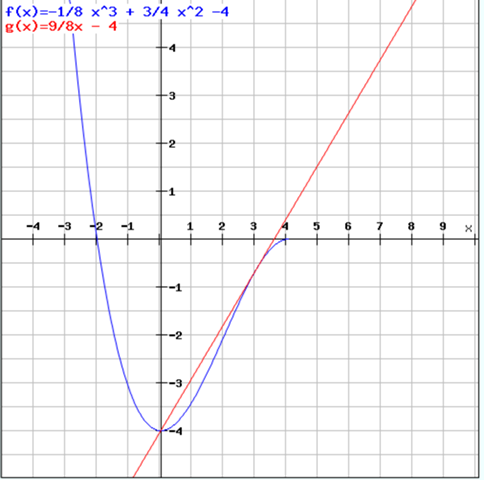
Nun gilt für den Ballon wenn er die Bedingung erfüllt und sich am Punkt xs befindet:
g(xs) = 2
2 = 9/8 xs - 4
9/8 xs = 6
xs = 5,33