Substitution mit x^6?
F(x)= x^6-5x^3+4
ich komme am Ende jedes Mal auf mehr als 2 nullstellen obwohl diese Funktion nur 2 hat.. kann mir bitte jemand die nullstellen ausrechnen und erklären wie ich das machen muss ?
2 Antworten
Hallo,
Substitution x³=z führt zur quadratischen Gleichung z²-5z+4=0, was zu
(z-1)*(z-4)=0 umgeformt werden kann.
Nullstellen bei z=1 und z=4 (auch über pq-Formel zu erhalten).
x³=1 oder x³=4. Reelle Nullstellen also bei 3. Wurzel aus 1 oder 3. Wurzel aus 4.
Die restlichen Nullstellen sind komplex.
Herzliche Grüße,
Willy
Nicht x^6 substituieren sondern x^3
Nachtrag:
Dann hast du an einer anderen Stelle falsch gerechnet.
Substitution mit z=x^3 funktioniert und ergibt mit
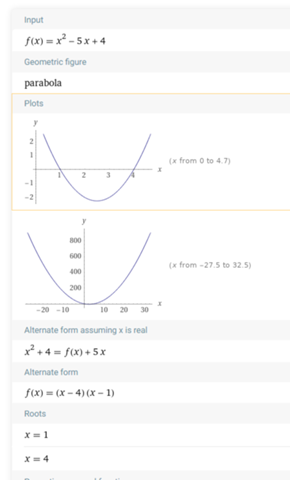
f(z)=z²-5z+4
eine schicke quadratische Funktion mit zwei reellwertigen Nullstellen.
ja was mich verwirrt ist, wieso nur 2 nullstellen ??
Die anderen 4 Nullstellen der originalen Funktion sind komplexwertig.
Siehe Antwort von Willy.
zu beachten aber, dass man hier eine neue Variable benutzen muss.
z=x^3
Dann ist f(z)=z^2-5z+4
Damit kommen wir dann an die Nullstellen für f(z).
Aus den sich ergebenden z müssen wir dann noch die 3. Wurzel ziehen. DAS sind dann die Werte für x.
Ich bin davon ausgegangen, daß die Fragerin mit der Technik der Substitution vertraut ist.
ja hab ich ja gemacht