Stimmt meine Antwort : Augensumme,?
Zu Teil a) welche Augensumme ...bis ... häufig?
A
Antwort:selten--->1/1;2/2;3/...bis..6/6
häufig---> außer diese 1/1;2/2;3/...bis..6/6. Stimmt Teil a?
Jetzt Antwort zu Teil d:: es fällt mir auf , dass bei 2 100 Mal geworfen wird, bei Aufgabe 5 ist nur 50 Mal.
Was könnte noch auffallen?
Aufgabe 2 Mit Lösung befindet sich unten.
Lösung no 5
diese sine die Augensumme der 2 Würfel
Lösung no 5
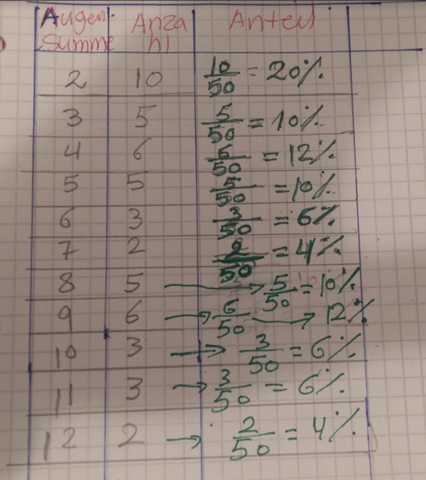
Lösung no 5
Aufgabe 2
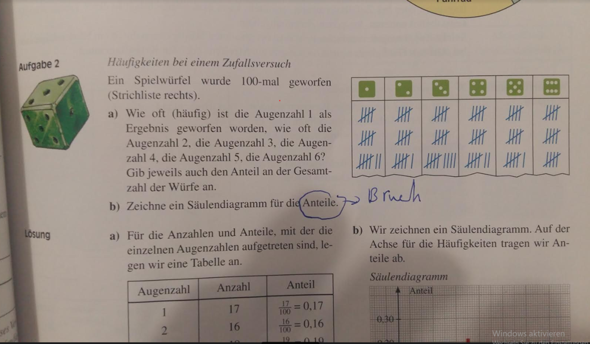
Aufgabe 2
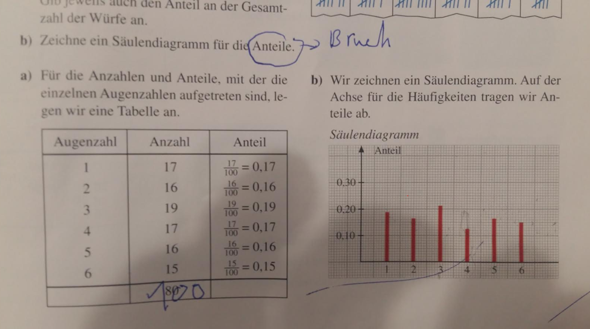
>in der ersten Zeile steht. Zwei spiewürfeln sollen gleich 50-mal....bis...
werden
diese sind 2 Würfeln, also sie sind gleichzeitig gewürfelt sind, warum zähle ich für Augensumme 3 ´ 2 Möglichkeit? (1+3; 3+1) ? die Reihenfolge hier macht keinen Sinn
wenn ich verstehe, wenn aber NUR eine Würfel, dann JA denn es kann 3 und 1
oder 1 und 3 , aber dies sind 2 Würfeln, deswegen es ist egal es sind NUR Summe
(1und 2) sie werde gleich gewürfelt
hier klares Foto von Aufgabe 5
es geht jetzt um Teil d)
Bild no 9
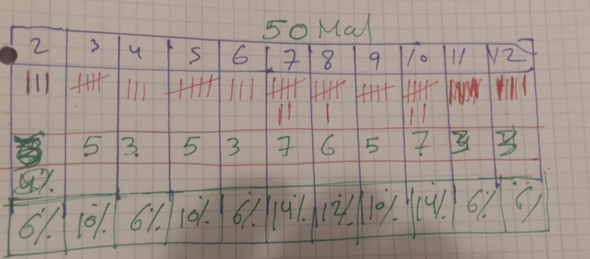
Bild 10
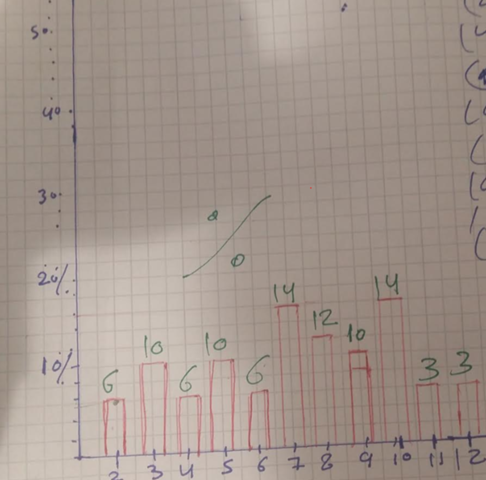
BIld 11
Aufgabe 5
1 Antwort
Du hast tatsächlich bei 50-mal würfeln 10-mal die Augensumme 2 gewürfelt, also (1|1)??? Ich glaube Deine Würfel sind gezinkt!!
Eigentlich sollte 2 (=1+1) und 12 (=6+6) am seltensten sein, da es für diese Summe nur eine Möglichkeit gibt; für die Summe 7 z. B. gibt es die Möglichkeiten (1+6;2+5;3+4;4+3;5+2;6+1), d. h. es sollte deutlich häufiger 7 als Summe rauskommen als 2!
Die 2 kannst Du nur mit 1|1 würfeln → 1 Möglichkeit
Die 3 kannst Du mit 1|2 und 2|1 würfeln → 2 Möglichkeiten
Die 4 kannst Du mit 1|3, 3|1 und 2|2 würfeln → 3 Möglichkeiten
Die 5 kannst Du mit 1|4, 4|1, 2|3 und 3|2 würfeln → 4 Möglichkeiten
Die 6 kannst Du mit 1|5, 5|1, 2|4, 4|2 und 3|3 würfeln → 5 Möglichkeiten
....
Die 11 kannst Du mit 5|6 und 6|5 würfeln → 2 Möglichkeiten
Die 12 kannst Du nur mit 6|6 würfeln → 1 Möglichkeit
2) Zweite Frage : wichtig. also weil es NUR ein Würfel ist wird also 2 mal hintereinander gewürfelt, deswegen zählst du auch so(4+3) eine Möglichkeit aber auch (3+4) also 2 ,oder?
Zweimal mit einem Würfel nacheinander würfeln und die Punkte zusammenzählen
ist das Gleiche wie einmal mit zwei Würfeln gleichzeitig würfeln
diese sind 2 Würfeln, also sie sind gleichzeitig gewürfelt sind, warum zähle ich für Augensumme 3 ´ 2 Möglichkeit? (1+3; 3+1) ? die Reihenfolge hier macht keinen Sinn
wenn ich verstehe, wenn aber NUR eine Würfel, dann JA denn es kann 3 und 1
oder 1 und 3 , aber dies sind 2 Würfeln, deswegen es ist egal es sind NUR Summe
(1und 2) sie werde gleich gewürfelt
Wenn Du mit 2 Würfeln würfelst, kann der eine Würfe eine 1 oder eine 3 haben, der ander aber auch. Also gibt es die Paare 1|1 oder 1|3 oder 3|1 oder 3|3.
Also gibt es bei einem Wurf 2mal die Möglichkeit? (1+3; 3+1)
also du meinst bei Augenzahl 3 , wenn ich 2 Würfel gleichzeitig würfele., kann sein dass diel erste Würfel die Augenzahl (1) und die zweite Würfel die Augenzahl(2) ,oder die erste Würfel die Augenzahl(2) und die zweite Würfel die (1) zeigt und in deine Fällen ist die Augensumme immer (3). ist Das was du meinst oder?
Es geht um hier um die Aufage 5 Teil a) zu beantworten
Zusammenfassung. kann ich so antworten.
** selten sind Augensumme: 2,12
**häufig sind alle anderen Augenzahlen (3,4,5,6,7,8,9,10,11) außer die (2,12).Reicht so ? , auch wenn einige mehr Möglichkeiten haben als andere? BSP 3(1+2 oder 2+1) _ 2 Mög.
aber Beis 4( 2+2 oder 3+1. oder 1+3) also 3 Mög. ich meine zu häufige Augensumme gehören alle diese (3,4,5,6,7,8,9,10,11)?
Die Summen 2 und 12 sind sehr selten, da es hier jeweils nur eine Möglichkeit gibt diese zu würfeln; bei 3 und 11 gibt es je 2 Möglichkeiten, diese Summen sollten also etwas häufiger auftreten; trotzdem kann man nicht von häufig sprechen. Am häufigsten sollte Augensumme 7 erscheinen; etwas weniger häufig 6 und 8, usw.
also exact die Antwort für Teil a)
ich antworte : selten Augenzahlen:2,12? nur das
häufig sage : am häufigstens sind 7 dann 6 und 8 und usw..... bis 3 und 11. also diese 6,8,5,4,9,,10,3,11 gehören AUCH zu häufig, oder es gibt gibt Augensumme( wie 3,11, oder ..) die weder selten noch häufig sind?
Es gibt hier keine EXAKTE Antwort. Ich würde es so machen: Die Augensummen 2 und 12 sind selten zu erwarten; die Augensumme 7 dagegen häufig.
Ob man da jetzt noch 6 und 8 zu "häufig" hinzuzählt ist Ansichtssache; alle anderen Summen würde ich weglassen, d. h. diese sind weder selten noch häufig.
ja, eine Summe, die man auf 6 verschiedene Arten würfeln kann (wie es nur bei der 7 der Fall ist), sollte logischerweise häufiger auftreten, als eine Summe, für die es weniger Möglichkeiten gibt; und umgekehrt sollte eine Summe für die es nur eine Möglichkeit gibt zu erwürfeln am seltensten auftauchen...
wenn alles geht kannst du Teil d) helfen . ? ich habe oben neues klares Bild von Aufgabe no 5 und Teil d rot markiert. Er sagt vergleiche Teil d in Aufgabe 5 mit der Aufgabe no 2 , und sag: was fällt dir auf?
Ich habe Teil so beantwortet :Es fällt mir auf , dass bei Aufgabe (2) 100 Mal geworfen wird, bei Aufgabe 5 ist nur 50 Mal.
reicht das , oder fällt dir etwas och auf?
Wie oft gewürfelt wurde ist für den Sinn des Themas eigentlich uninteressant, zumal an den Säulen nicht erkennbar ist, wie oft gewürfelt wurde!
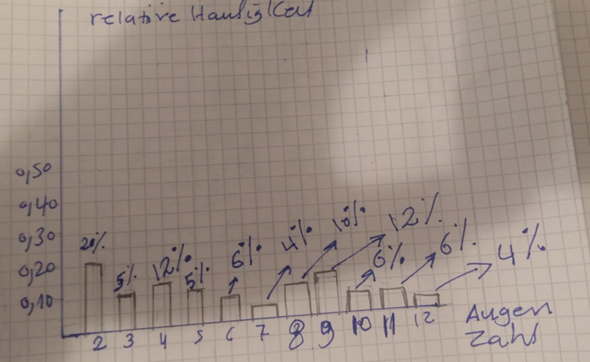
Es sollte auffallen, dass die Säulen beim Würfeln mit einem Würfel relativ nah beieinander liegen (also in etwa gleich hoch sind), da ja jede Wahrscheinlichkeit rechnerisch gleich ist; bei den Säulen mit den Augensummen sind die Höhen der Säulen unterschiedlich, weil nunmal die Wahrscheinlichkeiten unterschiedlich sind.
also du meint bei Aufgabe 2) würfeln mit einem Würfeln
ist die relative Häufigkeit=Warschienlichkeit bei allen is nicht größ unterschiedlich und deswegen stehen die Säulen fast gleich hoch.im gegen zu Aufgabe 5 ,wo mit 2 würfeln gewürfelt sind , da die relative Häufigkeit ziemlich gross undterschieldlich ist(20 % und 4 &) daher haben die Säulen größe Unterschiede in der Höhe, stimmt?
Ja, so meine ich das. Wobei Deine 20% für Augensumme 2 kann nicht richtig sein, wenn die Würfel in Ordnung sind. Wir haben doch festgestellt, dass Summe 2 am seltensten sein muss; bei Dir kam sie deutlich häufiger als alle anderen Summen!!
Die Säule bei Summe 7 müsste am größten sein, und zu den Seiten müsste sie kleiner werden, da die Wahrscheinlichkeiten kleiner werden.
aber wer weiß, vielleicht wenn ich mit 2 Würfeln würfele, kann sein dass es Beispeil, 20 mal beispiel diese Augenzahlen kommen
(1.1.) (1.1) (1,1) usw weiste also 20 Mal bei Würfel kommen IMMER diese (1,1) , dann muss ich diese 20 /50 *100 =20% in Säulendiagramm zeigen, oder?Ja wir haben theoritisch die Warscheinlichkeit von 7 ( 2+5; 6+1. usw,,,) am meistens, aber bei wirklichen würfeln, viellieciht kommen diese selten vor ,oder?
Frage 5) wichtig : in Teil b : sagt er führe den Zufall Versuch durch.... bis Ende. das bedeutet ich soll muss würfeln dann das Ergebnis in Diagramm eintragen. angenommen habe ich 20 mal die Augensumme 2 (1,1) gewürfelt, auch wenn es unwahrscheinlich ist ,dann kann ich dieses Ergebnis in Diagram eintragen. Also welche Ergebnis soll in Diagramm als Säule eingetragen werden?
ist das was wir diskutiert in Teil a? oder soll ich das Ergebnis in Teil b) machen und dann dieses Ergebnis dann in Diagramm als Säulen eintragen? diese Fage ist mir wichtig zu wissen.
wenn ich richtig versteh, werde ich weiter machen und dir die finale Antwort geben
3) Frage no 3: warum beispiel bei Augensumme 7 ,zählst du ( 1+6) und (6+1)ich meine oben steht das sind 2 Würfeln gleichzeitig gewürfelt, also Reihenfolge macht keinen Sinn, oder denke ich. was denkst du?
Für eine so simple Aufgabenstellung so viele Fragen zu stellen ist schon "erstaunlich" (um es mal nett zu umschreiben).
Dass die Reihenfolge nicht nur Sinn macht, sondern wichtig ist, d. h. dass es z. B. 1I3 und 3I1 als 2 verschiedene Möglichkeiten gibt um auf Summe 4 zu kommen, hat Geograph Dir schon richtig beantwortet. Jede andere Meinung ergibt keinen Sinn! Hier werde ich auch nicht weiter drauf eingehen bzw. darüber rumdiskutieren!
Ebenso macht es überhaupt keinen Sinn bei so einer Aufgabe, bei der es darum geht den Lernenden auf praktische Weise (hier durch eigenes Würfeln) an die Wahrscheinlichkeitsrechnung heranzuführen, sich einfach irgendwelche Ergebnisse auszudenken!?!?!
Diese Aufgabe 5 ist so aufgebaut:
a) Du sollst Dir selbst LOGISCH Gedanken machen, was wohl selten und was häufig als Summe rauskommt, wenn man 50-mal mit 2 Würfeln würfelt. Das haben wir hier die ganze Zeit besprochen (zu lange besprochen!).
b) hier soll durch die Praxis (eigenes Würfeln) die bei a) gemachte Vermutung überprüft werden. Dass 50-mal würfeln und eine Strichliste zu führen Dir zu lange dauert, klingt wie ein Witz, wenn man sieht, wie lange Du Dich mit all Deinen Aufgaben beschäftigst!
c) hier sollst Du aus Deiner Strichliste aus b) eine Tabelle erstellen, in der Du für jede Summe die Anzahl für deren Erscheinen und die entsprechende Wahrscheinlichkeit eintragen sollst
d) hier sollst Du die Wahrscheinlichkeiten aus c) in ein Säulendiagramm übertragen
Also Teil a) ist gemeint bei 2 kann nur (1+1),also Nur eine Möglichkeit bei 3 auch (2+1) auch nur eine Möglichkeit , oder bei 12(6+6) also auch Nur eine Möglichkeit, dann auch 11(5+6)oder? . also kann ich jetzt sagen 2,3,11,12 sind am selten?