Spannungsteiler Formel umstellen?
Ich möchte U1 berechen... irgendwie komme ich mit Addition durcheinander.
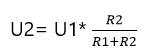
U2 = U1R2/R1+R2 - :U1
U2/U1 = R2/R1+R2 - :U2
1/U1 = R2/R1+R2U2 - dann? was mit 1?
6 Antworten
Tja da hättest du in Mathematik besser aufpassen müssen, als es noch um die Äquivalenzumformung ging :D machen wir einen kleinen Crashkurs:
Du kannst dir eine Gleichung vorstellen wie eine Wage. Auf beiden Seiten vom Gleichzeichen muss ausgerechnet das selbe Ergebnis stehen.
2*5=20/2
wir sehen, wenn wir 2*5 ausrechnen bekommen wir 10 und wenn wir 20 durch 2 teilen bekommen wir wieder 10, das passt also auf beiden Seiten steht das gleiche Ergebnis. Wenn wir umstellen darf das was links ausgerechnet rauskommt sich nicht von dem unterscheiden was rechts ausgerechnet raus kommt.
Wenn wir nach 20 umstellen müssen wir also logischerweise auf der Linken Seite mit 2 Multiplizieren:
2*5*2=20
passt. Denn wenn wir links ausrechnen kommt auch wirklich 20 raus. Damit ist die Waage immer im Gleichgewicht weil links in der Waagschale genauso viel drin ist wie rechts.
Mit Multiplikationen ist es relativ einfach. Wir dürfen auch die Faktoren untereinander tauschen oder auch erst 2*2 ausrechnen, dann steht da:
4*5=20 passt ja auch.
wie sieht es jetzt mit Additionen und Subtraktionen aus?
2*5=5+5
lösen wir nach 5 auf, so müssen wir lediglich 5 vom Ergebnis aus 2*5 abziehen also das Vorzeichen ändert sich und die 5 geht auf die andere Seite:
2*5-5=5 Wir haben immer gewisse Matheregeln mit denen wir rechnen müssen hier z.b. gilt jetzt Punkt vor Strich. das heißt wir dürfen nicht 5-5 rechnen und dass dann mit 2 Multiplizieren. Wir müssen erst 2*5 und dann das Ergebnis was ja 10 ist -5 rechnen, dann kommen wir auch auf unsere 5.
20=80/1+3
befindet sich die Addition unter dem Bruchstrich oder über dem Bruchstrich ist es so, als würde das was oben und das was unten steht in klammern stehen also:
(80):(1+3)
Das was in der klammer steht muss also zuerst ausgerechnet werden.
Lösen wir nach 3 auf. hier müssen wir das was in der Klammer steht also in dem Fall die 1+3 die wir in Klammern setzen als ein Faktor behandeln. Dann gelten für diesen "Faktor" erstmal die gleichen Regeln wie für andere Faktoren auch. Wir dürfen also den "Faktor" auf der Linken Seite an multiplizieren. damit der auf der rechten Seite verschwindet:
20*(1+3)=80
nun wird erst 1+3 gerechnet und dann das Ergebnis mit 20 Multipliziert und wir kommen dann insgesamt auf 80 passt also.
um jetzt nach 3 auflösen zu können müssen wir die Klammer loswerden. Klar können wir eine Klammer auflösen indem wir einfach sagen 20*1+20*3 denn das sind ja auch wieder 80. Aber ich finde es so tatsächlich eher umständlicher, ich würde einfach die 20 auf die andere Seite bringen:
1+3=80/20
dann ist auch die Klammer weg. um jetzt auf 3 zu kommen brauchen wir bloß die 1 rüber bringen, dadurch ändert sich das Vorzeichen und wir haben:
3=(80/20)-1
Vorsicht beim Kürzen!
20=79+1/3+1
viele neigen jetzt dazu einfach die +1 weg zu kürzen oder ähnliches in der Richtung. Das funktioniert so nicht, denn Additionsaufgaben hören auf andere Matheregeln als Multiplikationsaufgaben!
würde da stehen:
3=3+1-1
dann würde sich +1 und -1 rauskürzen.
genauso wie bei 80=80*2/2
dann kürzt sich die 2 weg.
Ganz allgemein kannst du dir auch merken: "Aus Summen kürzen nur die dummen."
aber auch hier gibt es ausnahmen:
20=80*4+80*4/2*4*4
Obwohl oben eine Summe steht dürfen wir in diesem Fall trotzdem eine 4 Kürzen. Vorraussetzung dafür ist, dass bei beiden Multiplikationen im Zähler mit der selben Zahl Multipliziert wird wie die Zahl durch die man im Nenner kürzen möchte. Hier ist es die 4 dadurch fällt oben im Zähler beide 4 ebenfalls weg und wir erhalten:
20=80+80/2*4
Ich habe das ganze hier jetzt mit Zahlen gemacht, damit man das Äquivalenzprinzip besser sieht, denn bei Äquivalenz geht es um Gleichheit, hier möchte man dafür sorgen, dass beim umstellen von Gleichungen auf beiden Seiten die "Waage" immer im Gleichgewicht ist.
Ersetzen wir die Zahlen jetzt durch Buchstaben, dabei handelt es sich einfach um Variablen, also einfach nur Platzhalter für eine Beliebige Zahl.
Wenn wir aber z.b. in der gleichung 2 a finden also a*a dann sollte klar sein, dass egal welche Zahl wir für a einsetzen für beide a die gleiche zahl eingesetzt wird. ist also a=4 dann hätten wir bei a*a eingesetzt 4*4.
a-b/a auch bei diesem Term ist es verlockend das a zu kürzen weil sie ja gleich sind aber oben im Zähler steht eine Summe oder Differenz und aus Summen kürzen nur die Dummen!
4-a/2 auch hier das selbe hier währe es verlockend 4/2 zu kürzen, denn das währe ja 2 und dann hätten wir 2-a aber auch hier: "Aus Summen kürzen nur die Dummen!" Wir haben im Zähler eine Summe oder Differenz.
8*(4-a)/2 jetzt darf ich kürzen 8/2 ist 4 also haben wir 4*(4-a)
oder a*(a-b)/a auch hier darf das a weg und a-b bleibt stehen, hier darf gekürzt werden ohne, dass sich das Ergebnis verändert.
Nun kommen wir zu deiner Aufgabe:
U2=U1*(R1/R1+R2)
Ich habe bewusst R1/R1+R2 ausgeklammert. Damit will ich Symbolisieren, dass U1 an den Bruch an multipliziert wird. Hier darfst du U1 mit in den Bruch werfen, falls es dir dann leichter fällt zu rechnen:
U2=U1*R2/R1+R2
Nun haben wir ja besprochen, dass wir die Summe aus den Summanden R1 und R2 im Nenner zusammen als ein gemeinsamen Faktor betrachten müssen. So können wir diesen "Faktor" einfach genauso behandeln wie jeden anderen auch, hier brauchen wir nichts auszuklammern, denn die Variablen innerhalb der Klammer also unsere jeweiligen Summanden interessieren uns in dem Fall nicht, wir wollen nur U1.
U2*(R1+R2)=U1*R2
Jetzt brauchen wir nur noch das was Links steht komplett durch R2 zu teilen und wir haben U1:
U2*(R1+R2)/R2=U1
Bei dir hast du zum einen das ganze etwas umständlich gemacht, denn es währe leichter wenn wir U1 im Zähler lassen, denn diese Größe wollen wir ja, der Kehrwert also 1/U1 den wollen wir ja jetzt nicht unbedingt.
außerdem hast du R1+R2*U2 im Nenner gemacht. Das geht nicht, denn Punkt vor Strich. R1+R2*U2 bedeutet, dass wir erst U2*R2 ausrechnen müssen und das Ergebnis dann mit R1 addieren. Und das Ergebnis davon ist ja ein anderes wie als wenn ich erst R1+R2 ausrechne und das Ergebnis dann mit U2 multipliziere. Also muss ich R1+R2 in Klammern setzen:
(R1+R2)*U2.
U2=U1*(R2/(R1+R2)) dividiert durch (R2/(R1+R2))
U2/(R2/(R1+R"))=U1
U1=U2*(R1+R2)/R2 man teilt einen Bruch durch einen Bruch,indem man ihn mit dem Kehrwert mal nimmt
(U2/1)/(3/4)=U2/1*4/3=4/3*U2
so macht man es sich einfacher :
Man nennt den Bruch einfach mal b .
Dann steht da
U2 = U1 * b >>>> U2 / b = U1
jetzt muß man nur noch wissen, das 1/4 durch 3/4 = 1 * 4 / 4 * 3 ist (malnehmen mit Kehrwert )
Drum
U1 = U2 * (R1+R2)/R2 .....
- multipliziere erst mit (R1+R2)
- dividiere dann durch R2
Alles mit Umkehrbruch multiplizieren. R2 darf dabei nicht 0 sein.