Simple, jedoch unlösbare Matheaufgabe?
Folgende Aufgabe bereitet uns und gerade unserem Lehrer Kopfzerbrechen... Eine Simple Sachaufgabe, bringt uns an unsere Grenzen.
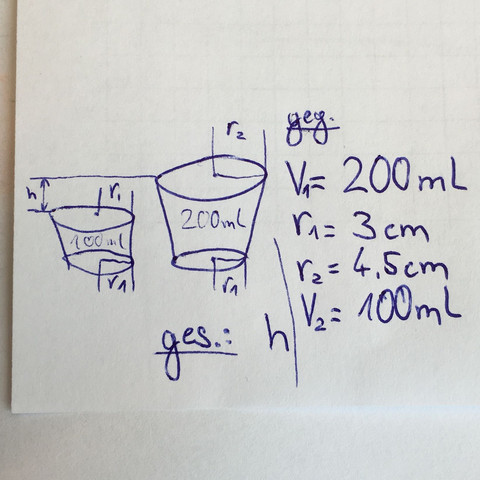
Ein kegelstumpfförmiger Becher ist mit 200ml einer Flüssigkeit gefüllt. Um wie viel cm muss sich der Wasserstand verringern, wenn ich genau 100ml abgießen, bzw. behalten möchte?
Weitere Informationen entnehmt bitte des Bildes unten.
Schon mal vielen Dank im Voraus für eure Hilfe!!! ❤️
6 Antworten
- Berechne die Höhe h beim gefüllten Becher mit Hilfe des Volumens.
- Berechne phi mit Hilfe der Höhe h und der beiden Radien R und r (in deinem Fall r2 und r1).
- Ersetze R in der Volumen-Gleichung durch R=(h*tan(phi))+r
- Berechne die neue Höhe aus dieser veränderten Volumen-Gleichung.
https://de.wikipedia.org/wiki/Kegelstumpf#Formeln
So sollte es klappen.
Hallo,
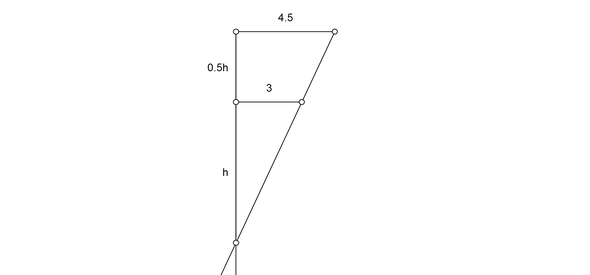
zunächst machst Du Dir eine Zeichung wie die Skizze, die ich hochlade. Es handelt sich um den halben Querschnitt des Bechers, der zu einem rechtwinkligen Dreieck ergänzt wurde.
Du hast die zwei Radien von 3 und 4,5 cm Länge.
Nach dem Strahlensatz ist die Höhe des Kegelstumpfes halb so hoch wie die Höhe von der Kegelspitze bis zum kleineren Radius.
Nun weißt Du, daß der Kegelstumpf ein Volumen von 200 ml besitzt.
Es gilt also:
1,5h*π/3*4,5²-h*π/3*3²=200
Wenn Du h ausklammerst, bekommst Du:
h*(1,5*π/3*4,5²-π/3*3²)=200
h=200/(1,5*π/3*4,5²-π/3*3²)=8,935 cm
Die Höhe des Kegelstumpfes ist die Hälfte davon, also 4,4675 cm.
Nun kannst Du das Volumen des Bechers berechnen, wenn es sich um einen kompletten Kegel handeln würde. Es sind die 200 ml des Kegelstumpfes plus dem Kegel, den Du unterhalb dieses Stumpfes angesetzt hast. Dessen Volumen beträgt π/3*3²*8,935=84,21 ml.
100 dazu macht 184,21 ml.
Nun mußt Du die Höhe und den Radius eines Kegels bestimmen, dessen Volumen 184,21 ml beträgt und die sich genauso zueinander verhalten, wie Höhe und Radius des kompletten Kegels. Dieses Verhältnis ist leicht zu bestimmen, nämlich 8,935:3=2,978
h=2,978r
Nun kannst Du eine Gleichung mit einer Unbekannten, nämlich r, aufstellen:
π/3*r²*2,978r=184,21
r³=184,21/(π/3*2,978)=59,069
r=3,895
h=3,895*2,978=11,599
Das ist die Höhe des kompletten Kegels mit dem Volumen 184,21 ml.
Um die Höhe zu bestimmen, bis zu der der Becher gefüllt sein muß, damit er nur 100 ml enthält, mußt Du davon noch die Höhe des Kegels bis zum Radius 3 cm abziehen: 11,599-8,935=2,664 cm.
Das ist die gesuchte Füllhöhe.
Herzliche Grüße,
Willy
Das scheint mir machbar, wenn man den dazugehörigen richtigen Kegel bestimmt (und da euer Lehrer euch unterstützt, muss ich es nicht bis ins Detail ausrechnen).
Mit der Kegelstumpfformel
V = (h π/3) * (r₁² + r₁r₂ + r₂²)
ist die Höhe h der Flüssigkeit im Kegelstumpf zu ermitteln:
h = (3 V) / (π (r₁² + r₁r₂ + r₂²))
Ich bezeichne die Höhe des umgedrehten Kegels bis zur Wasseroberfläche mit k. Dann kann ich mit dem 2. Strahlensatz k bestimmen:
k / (k - h) = r₂ / r₁ Für k etwas umformen:
k = r₂ h / (r₂ - r₁)
http://dieter-online.de.tl/Br.ue.che-1.htm Hilfe für Brüche
Die Berechnung der kompletten Volumina im gedachten Gesamtkegel müsste es dann ermöglichen, die gewünschten Höhenunterschiede herauszubekommen. Ggf. ist der Strahlensatz nochmals anzuwenden.
Wenn ich mich irgendwo verdaddelt habe, müsstet ihr es beim Nachvollziehen sofort merken können. Es kommt ja nur auf das Prinzip an. Und das läuft hier über den Gesamtkegel und den Strahlensatz.
Spontane Idee:
Den Kegelstumpf zu einem ganzen Kegel ergänzen. Dann 2. Strahlensatz.
Diese Angabe ist ohne Gewähr :-))
Auf die Idee sind wir auch gekommen jedoch fehlt uns in dem Fall r, bzw. die Höhe vom kleineren Volumen
Habt Ihr es inzwischen raus? Sonst bleibe ich gleich mal am Ball, äh Becher...
Mein Tipp Volumen des bechers, Volumen von Wasser ausrechnen, und vie viel cm3 an Wasser auf den Durchmesser mit der Breite von 1 quadratcm entfällt. Als formberecunug ein cylinder nehmen, das Volumen des Wassers im cylinder berechnen, und das wasservolumen abziehen von den Becher. Auf dieser Art habt ihr eine exakte Berechnung des volumenwassers trotz unperfekter Form des bechers bei einer unvollständigen Füllung
.vieleicht als gedankenstütze für dein Lehrer...
100 ml abgießen, rand messen.. Habt ihr schon das Endergebniss und vieleicht kann dein Lehrer mit dem was anfangen
Ich hätte dich erst kontaktieren sollen, Willy. Dass du parallel zu mir dasselbe Thema aufgreifst, konnten wir natürlich beide nicht ahnen.