Schweren Grenzwert berechnen?
Ich habe größerwerdende Zahlen eingesetzt und die Funktion scheint gegen e zu gehen für x gegen Unendlich. Aber wie beweise/zeige ich das formell mathematisch?
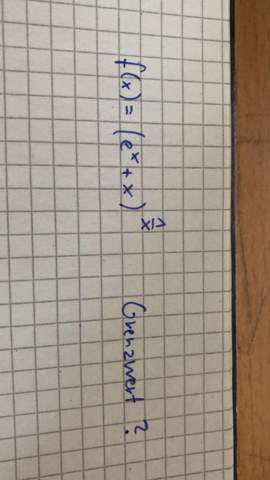
3 Antworten
Minoranten-Majoranten-Kriterium; Monotonien nutzen
Für x > 1 ist
e < (e^x + x)^(1/x) < (x e^x + x)^(1/x)
Dann zeigen (oder nutzen, falls bereits gezeigt), dass
2^(1/x)
und
x^(1/x)
für x -> +unendlich gegen 1 konvergieren
Sorry. Das war mein erster Ansatz.
Richtig wäre
Für x > 1 ist auch e^x > 1 und damit
e < (e^x + x)^(1/x) = (1 * e^x + x * 1)^(1/x) < (x e^x + x e^x)^(1/x)
Wenn man eine Minorante und eine Majorante hat, die beide konvergieren, liegen alle Häufungspunkte der betrachteten Folgen zwischen diesen beiden Grenzwerten (einschließlich).
Wenn Minorante und Majorante denselben Grenzwert haben, bleibt der betrachteten Folge nichts anderes übrig, als ebenfalls diesen Grenzwert zu haben.
ich glaube das checke ich heute nicht mehr trotzdem danke für ihre antwort. Ich verstehe ehrlich gesagt nicht wie die majorante und minorante gegen e konvergieren sollen
gibt es andere möglichkeiten den grenzwert zu bestimmen? oder es irgendwie so umzuformen dass man l´hospital anwenden kann?
Die Konstante e konvergiert natürlich gegen e.
Die rechte Funktion lässt sich faktorisieren - in x^(1/x) * 2^(1/x) * e
Nutze 0 ≤ x ≤ eˣ:
- (eˣ + 0)¹'ˣ = e
- (eˣ + eˣ)¹'ˣ = 2¹'ˣ·e → e
und f liegt für x≥0 immer zwischen den beiden.
Nutze, dass x langsamer wächst, als e^x
Das ist mir klar, trotzdem verstehe ich nicht wieso e der Grenzwert ist? bzw. wie kann ich es MATHEMATISCH erklären?
also ist e doch nicht der grenzwert?