Schnittgerade von Ebenen in KOORDINATENFORM?
Hallo,
seit Stunden versuche ich zu verstehe, wie man die Schnittgerade von 2 Ebenen in Koordinatenform berechnen kann.
Als Bsp:
- 2y-2z=4
- 2x+2y=4
Ich habe schon versucht y zu eliminieren und am Ende x=z rausbekommen.
Bin todes verzweifelt hilfee 😑
6 Antworten
Ich würde da so vorgehen:
Ebenengleichungen gleichsetzen:
2y-2z = 2x+2y
z = -x
aus 2x+2y=4 folgt:
y = 2 - x
Nun brauche ich zwei Punkte, um die Gerade durchzulegen. Dazu nehme ich ein beliebiges x an, aber so, dass es bequem wird:
Aus x = 0 folgt:
y = 2
z = 0
Aus x = 1 folgt:
y = 1
z = -1
Den ersten Punkt nehme ich nun als Stützvektor (0/2/0) und den Richtungsvektor berechne ich aus P2 - P1:
(1/1/-1) - (0/2/0) = (1/-1/-1)
und damit lautet die Geradengleichung:
g: x = (0/2/0) + r(1/-1/-1)
Ebene E1 oder E2 in die vektorielle Parametergleichung der Eben
E: x=a+r*u+s*v umwandeln
1) kann man direkt machen → nehmen wir mal E1
Normalenvektor n(0/2/-2)
nx=0 und ny=2 und nz=-2
ux=ny=2
uy=-1*nx=-1*0=0
uz==0
u(2/0/0)
vx=0
vy=nz=-2
vz=-1*ny=-1*2=-2
v(0/-2/-2)
E1: x=a+r*(2/0/0)+s*(0/-2/-2)
Probe: u kreuz v=n
(2/0/0) kreuz (0/-2/-2)=n(0/4/-4) →dividiert durch 2 → n(0/2/-2) stimmt
2) 3 Punkte auf der Ebene berechnen zum Beispiel z=1 → y=(4+2)/2=3
Dreipunktgleichung der Ebene E: x=a+r*(b-a)+s*(c-a)
A(ax/ay/az) → Ortsvektor a(ax/ay/az)
B(bx/by/bz) → Ortsvektor b(bx/by/bz)
C (cx/cy/cz) → Ortsvektor c(cx/cy/cz)
Richtungsvektor m von Punkt A nach Punkt B → b=a+m → AB=m=b-a
Richtungsvektor m von Punkt A nach Punkt C → c=a+m → AC=m=c-a
E: x=a+r*(b-a)+s*(c-a) ergibt dann die vektorielle Parametergleichung der Ebene
E: x=a+r*u+s*v
u(ux/uy/uz)=(bx/by/bz)-(ax/ay/az)
v(vx/vy/vz)=(cx/cy/cz)-(ax/ay/az)
Die vektorielle Parametergleichung in die Ebene E2: 0*x+2*y+2*z=4 einstzen und nach den Parameter s=... umstellen
dann s=.. in die Vektorielle Parametergleichung der Ebene einsetzen,ergibt dann
eine Gerade der Form g: x=a+r*m ist die Schnittgerade der beiden Ebenen.
Hinweis: 2 Ebenen sind parallel,wenn die beiden Normalenvektoren parallel sind
n1*t=n2
oder der Normalenvektor der einen Ebene n1(n1x/n1y/n1z) steht senkrecht auf den beiden Richtungsvektoren u(ux/uy/uz) und v(vx/vy/vz) der anderen Ebene E2.
Den Rest schaffst du selber.
Hast mich auf eine gute Idee gebracht.Es geht.
gegeben: 2 Ebenen
E1: 1*x+2*y+3*z+10=0
E2: -2*x+1*y+4*z-20=0
wir brauchen nun 2 Punkte,die gleichzeitig auf E1 und E2 liegen
wir haben hier ein lineares Gleichungssystem (LGS) mit 3 Unbekannte,x,y und z
1) 1*x+2*y+3*z+10=0
2) -2*x+1*y+4*z-20=0
es gibt hier unendlich viele Lösungen.Wir wählen frei z=1
1) 1*x+2*y=-10-3=-13
2) -2*x+1*y=20-4=16
Lösung mit meinem Graphikrechner (GTR,Casio) x=-9 und y=-2
P1(-9/-2/1)
Eine Probe ergibt:P1 liegt auf beiden Ebenen gleichzeitig
nun wählen wir frei z=5
1) 1*x+2*y=-10-15=-25
2) -2*x+1*y=20-20=0
Lösung mit meinen GTR ,x=-5 und y=-10
P2(-5/-10/5)
liegt auch gleichzeitig auf Ebene E1 und E2
Damit haben wir 2 Punkte,um die Schnittgerade zu berechnen
Gerade g: x=(-9/-2/1)+r*[(-5/-10/5)-(-9/-2/1)]
x=(-9/-2/1)+r*(4/-8/4) → m(4/-8/4) dividiert durch 4 → m(1/-2/1)
Schnittgerade g: x=(-9/-2/1)+r*(1/-2/1)
Prüfe auf Rechen und Tippfehler.
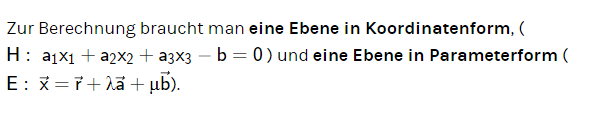
ich erinnere mich nur dunkel , aber wenn du das
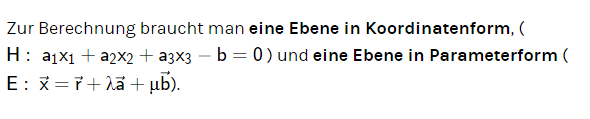
darfst , dann versuch es mal anhand dieser Anleitung .
(umwandlung Ko in Par - Form unten auf der Seite )
haha danke. Ich wollte es unbedingt mit der Koordinatenform lösen ohne die Parameterform.
Übungsbeispiel:gegeben 2 Ebenen
E1: x=(0/0/3)+r*(3/2/-1)+s*(3/0/-1)
E2: 4*x+3*y+6*z=36
Ebene E1 in E2 einstzen
mit E1
x-Richtung: x=0+r*3+s*3
y-Richtung: 0+r*2+s*0
z-Richtung: 3+r*(-1)+s*(-1)
in E2 eingesetzt und nach s umgestellt → s=3-2*r in E1 ergibt
Schnittgerade g: x=(9/0/0)+r*(-3/2/1)
hey erstmal danke. diesen weg kenne ich auch aber ich wollte es unbedingt lösen ohne die Parameterform also mit 2 Ebenengleichungen in Koordinatenform
Merke:Für jede Unbekannte braucht man eine Gleichung,sonst ist die Aufgabe nicht lösbar.
Du brauchst 2 Punkte P1(x1/y1/z1) und P2(x2/y2/z2),die auf beide Ebenen gleichzeitig liegen.
also E1=E2
a1*x+b1*y+z1*z+d1=a2*x+b2*y+c2*z+d2
setz mal z=1 dann hast du 2 Unbekannte x und y und 2 Gleichungen.
Probier mal ob das Funktioniert
Wenn du 2 Punkte hast,die beide gleichzeitig auf E1 und E2 liegen,dann hats du auch die Geradengleichung g: x=a+r*(b-a)
wir wählen frei z=1
LGS
1) 0*x+2*y-2*1=4
2) 2*x+2*y-0*1=4
1) 0*x+2*y=4+2=6
2) 2*x+2*y=4+0=4
Lösung mit meinem GTR x=-1/3/1)
Probe ergibt P1(-1/3/1) liegt auf beiden Ebenen
wir wählen z=2
1) 0*x+2*y=4+4=8
2) 2*x+2*y=4+0=4
Lösung x=-2 und y=4
P2(-2/4/2)
1) 0*-2+2*4-2*2=8-4=4 stimmt
2) 2*(-2)+2*4-0*2=-4+8=4 stimmt
damit haben wir 2 Punkte,die auf der Schnittgeraden liegen
Schnittgerade g: x=(x1/y1/z1)+r*[(x2/y2/z2)-(x1/y1/z1)]
Ich danke dir. Ist es auch irgendwie möglich die Schnittgerade aus 2 Ebenen in Koordinatenform zu berechnen ohne es in PF umzuwandeln?