pH Wert Berechnung Säure - Base - Mischung?
Hallo Community,
Ich verstehe nicht wie man diese Aufgabe rechnen soll:
Welchen pH- Wert hat eine Mischung aus 110 ml 0.1M Schwefelsäure und 100 ml 0.025 M Natronlauge? Runden Sie das Ergebnis auf drei signifikante Stellen.
Wie geht man hier vor? Wie kann man bei Mischung aus Säure und Base den pH - Wert berechnen?
Danke im Voraus!😄
4 Antworten
110 ml 0.1M Schwefelsäure und 100 ml 0.025 M Natronlauge?
Wir brauchen nicht Konzentrationen, sondern Stoffmengen.
Wir haben 11 mMol H₂SO₄ und 2,5 mMol NaOH.
Jetzt kommt ein Schritt, den der Schüler eher nicht abschätzen kann, und den der Lehrer bei der Aufgabenstellung wohl übersehen hat:
Bei dem gesuchten (und erstmal auf 1 geschätzten) pH-Wert dissoziiert die Schwefelsäure nicht (bzw. nur zu 20%) zu 2 H⁺ und SO₄²⁻, sondern zu 1 H⁺ und HSO₄⁻
Nach der Reaktion (Neutralisation) bleiben daher 8,5 mMol H₂SO₄ und 2,5 mMol NaHSO₄. Die Volumina kannst Du als additiv betrachten und die Konzentration an Säure (ca. 0,04 mol/l) und Hydrogensulfat ausrechnen.
Jetzt kannst Du entweder (je nachdem, was Ihr gelernt habt) dies betrachten und berechnen als
- Lösung der starken Säure H₂SO₄ und das HSO₄⁻ ignorieren
- Puffermischung aus H₂SO₄ und HSO₄⁻
Der Unterschied ist nicht groß, eine Berechnung "drei signifikante Stellen" ergibt aber Unterschiede.
eine Mischung aus 110 ml 0.1M Schwefelsäure und 100 ml 0.025 M Natronlauge
Das muß gerade en vogue sein — ein ganz ähnliches Beispiel ich habe es erst vor ein paar Stunden vollständig durchgerechnet:
- Die Stoffmenge an Schwefelsäure ist n=cV=0.011 mol
- Die Stoffmenge an NaOH ist n=cV=0.0025 mol
- Das Ganze spielt sich in einem Gesamtvolumen von Vₜₒₜ=210 ml ab.
Wir haben mehr als viermal soviel H₂SO₄ als NaOH, also kann die Neutralisationsreaktion nur teilweise ablaufen:
H₂SO₄ + NaOH ⟶ NaHSO₄ + H₂O
Die 0.0025 mol NaOH können mit 0.0025 mol H₂SO₄ reagieren, daraus entstehen 0.0025 mol NaHSO₄, und 0.0085 mol H₂SO₄ bleiben übrig. Das alles spielt sich in 210 ml Volumen ab, also enthält die Lösung c(H₂SO₄)=c₁=n/V=0.0405 mol/l und c(NaHSO₄)=c₂=0.0119 mol/l.
In guter Näherung können wir annehmen, daß der pH-Wert von der H₂SO₄ allein bestimmt wird, daß wir also das NaHSO₄ vernachlässigen können. H₂SO₄ ist eine starke Säure in erster Dissoziationsstufe und mittelstark (pKₐ=2) in der zweiten.
- Wäre die Säure einbasig (gäbe es also keinen zweiten Dissoziationsschritt), dann könnte man den pH mit der Formel für starke Säuren berechnen: pH=−lg(c₁)=1.393
- Wenn wir den zweiten Dissoziationsschritt berücksichtigen wollen, dann müssen wir mit dem Massenwirkungsgesetz mit der Säurekonstante Kₐ=10¯ᵖᴷᵃ herumrechnen und erhalten pH = −lg[ ½(c₁−Kₐ) + √(¼(c₁+Kₐ)²+Kₐc₁) ] = 1.323
- Dabei haben wir den Beitrag des Hydrogensulfats vernachlässigt; eine genaue Rechnung ergibt pH=1.307, eine ziemlich vernachlässigbare Korrektur.
Welche Lösung Dein Lehrer sehen will, kann ich Dir nicht sagen. Wähl Dir das aus, das Dir am besten gefällt, runde es auf zwei Nachkommastellen und fertig.
Als Bonus gibt es noch die Gleichung, mit der man alle drei Resultate ausrechnen kann:
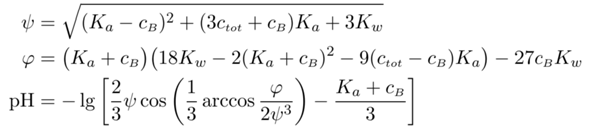
Dabei ist gemeint, daß Du entsprechend Deiner Problemstellung Kₐ, ctot und cB in die oberen beiden Gleichungen einsetzt, die beiden Hilfsgrößen φ und ψ ausrechnest und dann aus der dritten Gleichung den pH bekommst.
- Wenn Du die H₂SO₄ als stark und einbasig annehmen willst, dann setzt Du entweder ctot=0 und cB=−c₁ oder ctot=c₁ und cB=0 und Kₐ unrealistisch groß, z.B. 1000 mol/l, oder ctot=c₁ und cB=−c₁ und Kₐ unrealistisch klein, z.B. 10¯¹⁰ mol/l ⟹ pH=1.393
- Willst Du H₂SO₄ als zweibasig rechnen, aber das NaHSO₄ vernachlässigen, dann setzt Du ctot=c₁ und cB=−c₁ und die Säurekonstante auf den richtigen Wert Kₐ=10¯²=0.01 mol/l ⟹ pH=1.323
- Für die genauestmögliche Rechung ctot=c₁+c₂ und cB=−c₁ und Kₐ=10¯²=0.01 mol/l ⟹ pH=1.307
- Eine genaue Erklärung dieser Gleichung mag ich jetzt aber nicht geben.
c1=.0085/.210
c2=.0025/.210
ka=0.01
-l10(c1)
1.3928
phfull(c1,0,-3,14)
1.3928
phfull(0,-c1,2,14)
1.3928
phfull(c1,-c1,12,14)
1.3928
-l10(.5*(c1-ka)+sqrt(.25*(c1+ka)^2+ka*c1))
1.3232
phfull(c1,-c1,2,14)
1.3232
phfull(c1+c2,-c1,2,14)
1.3071
P.S.: Wegen ungenauen Lesens stand da vorher etwas ganz anderes.
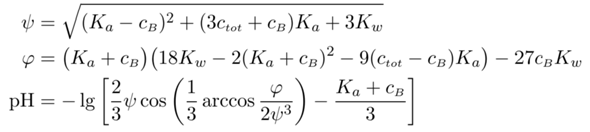
Danke, ich hab das Komma falsch gelesen und daher nicht den Unterschied zur verlinkten anderen Antwort bemerkt. Jetzt ist es hoffentlich richtig.
Anzahl der Mol H+ und OH- Ionen in den jeweiligen Lösungen berechnen.
Differenz der molaren Mengen berechnen.
PH Wert berechnen.
Nein, das Volumen muss noch berücksichtigt werden. Du hast eine erhebliche Veränderung des Volumens. Außerdem ist Schwefelsäure zweiprotonig
Was meinst du mit Differenz der molaren Mengen genau? Kannst di es mithilfe meiner Fragestellung beantworten?
Stelle zuerst die Reaktionsgleichung von Natronlauge mit Schwefelsäure auf. Nimm als Produkt der Einfachheit halber das neutrale Natriumsulfat an.
Berechne die in den Ausgangslösungen vorhandenen Stoffmengen der beiden Stoffe (n=c*V).
Berechne jetzt, unter Mitführung sämtlicher Einheiten und unter Berücksichtigung der Reaktionsgleichung die Stoffmengen beider Stoffe (in mol), die zur Reaktion verbraucht wurden.
Ziehe den Verbrauch von der Menge der Überschußkomponente ab. Im Folgenden kannst Du das Reaktionsprodukt ignorieren.
Berechne jetzt die Konzentration der Überschußkomponente im gesamten Volumen der vereinigten Lösungen.
Annahme: Im aktuellen Beispiel kannst Du von vollständiger Protolyse ausgehen. Das heißt, daß jedes Säureproton "lose" in der Lösung schwimmt und zum pH-Wert beiträgt.
Berechne die Hydronium-Konzentration in Mol pro Liter und rechne in den dekadischen Logaritmus um.
Schreibe bitte das Ergebnis in den Kommentar, daß Andere es überprüfen können.
Da ist mit Sicherheit ein Fehler drin.
Mein Ergebnis (grobe Schätzung, vereinfacht): Wir haben ca. 0,1mol H2SO4 in 0,2L Lösung. Da Schwefelsäure, gemäß meiner Annahme, vollständig protolysiert vorliegt haben wir 0,2mol H3O+ Ionen in der Lösung. Die 0,0025 mol Natriumhydroxid fallen unter "Rundungsfehler" bei meiner Schätzung. 0,2mol in 0,2L machen grob 0,1mol/L. Das kann man auch als "Zehn hoch minus eins" mol pro Liter schreiben und erhält einen pH-Wert, der um Eins liegen muß.
Das Ergebnis ist also weit genug vom Ionenprodukt des Wassers entfernt, daß wir dieses nicht berücksichtigen müssen, um innerhalb der geforderten Toleranz ein sinnvolles Ergebnis zu berechnen. Bei pH-Werten oberhalb von 4, bis unterhalb von 10 müßte man genauer rechnen.
Dein Ergebnis hat leider keine Maßeinheit, daß ich den Weg schlecht nachvollziehen kann. Führe bitte IMMER die Maßeinheiten mit, damit Du sie nicht verlierst oder in falscher Form aufschreibst. Gerade bei Konzentrationen und Stoffmengen kann man sich böse vertun, weil die Einheiten ähnlich lauten...
Das hatte ich vermutet. Jetzt müßtest Du mal nach meiner Anleitung die ganze Rechnung durchgehen, um den Gehler zu finden. Der kann überall stecken, sogar im letzten Schritt als Kommafehler...
Derzeit lautet die Aufgabe:
Da ist eindeutig die Säure im großen Überschuss.