Parabel g(x)=a-bx² soll Nullstellen berühren, bestimme a und b?
Hallo,
ich habe alle diese Aufgaben gerechnet und habe Probleme damit die Lösung von c) nachzuvollziehen. Ich selber habe eine andere Parabel aufgestellt die ebenso funktioniert jedoch würde ich die Lösung gerne verstehen für den Rechenweg. Kann mir jemand erklären was dort gerechnet wurde?
vielen Dank schonmal

2 Antworten
Ich selber habe eine andere Parabel aufgestellt die ebenso funktioniert
.
.
Es gibt unendlich viele Parabeln , die durch (-2/0) und (+2/0) gehen
.
Es gibt aber nur EINE Parabel , die die Bedingung "Berührung" erfüllt. Hast du andere Werte für a und b als in der Lösung, ist das leider nicht richtig .
.
g'(x) = f'(x)
-2bx = -2x³ + 4x
0 = -2x³ + 4x + 2bx
0 = -2x*(x² -2 - b )
mit x = 2
0 = -2*2(4-2-b)
0 = -4*(2-b)
0 = -8 + 4b
.
f(x) = g(x) mit x = 2
0 = a - 4b
4b = a
oben einsetzen
0 = -8 + a
8 = a
.
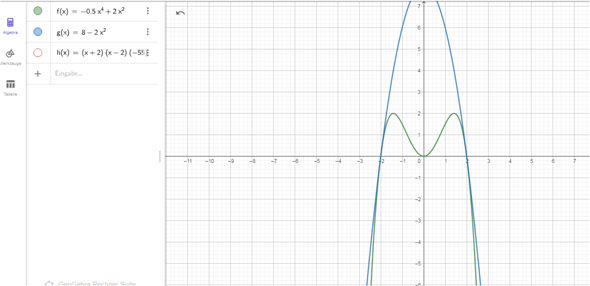
Das ist die richtige Parabel
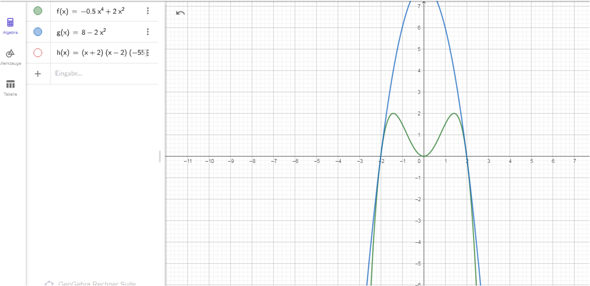
sie "umschmiegt" die grüne , sie berührt sie
Und hier eine der vielen , die nicht korrekt sind , obwohl sie durch die Nullstellen gehen
sie schneidet !
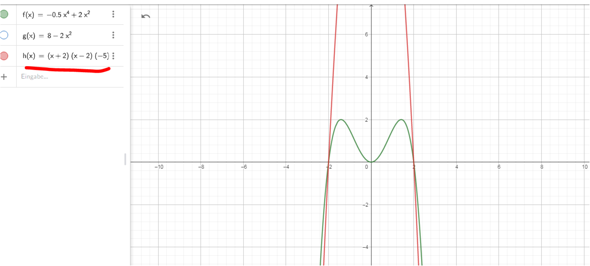
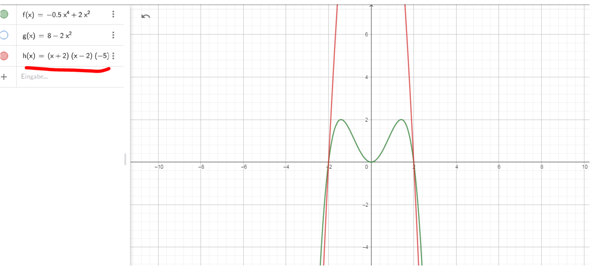
Berühren heißt in der Mathematik : gleiche Steigung . Das ist ganz eindeutig .
Ja , es gibt unendlich viele Parabeln, die durch die Nullstellen gehen
ich poste mal zwei Bilder
Naja damit g(x) f(x) berührt gibt es zwei Kriterien
- Die beiden müssen sich schneiden bzw den selben funktioswert an der selben stelle haben. Deswegen setzt man beide gleich also g(x)=f(x)
- Sie müssen die selbe Steigung an dieser Stelle haben.Deswegen f‘(x)=g‘(x)
Und was macht das „Berühren“ aus? Die läuft doch auch einfach nur durch die beiden äußeren Nullstellen😅 Und ist es egal von welchem Punkt, oder in diesem Fall Nullstelle, man den x-Wert einsetzt?