Mathehausaufgaben-wie weit ist die Sicht des Kapitäns?
Ein Kapitän befindet sich 25m über der Wasseroberfläche. Der Radius der Erde beträgt 6371km. Wie weit kann er bei klarer Sicht sehen?
Ich habe keinen Plan was ich machen soll...
3 Antworten
Eine Skizze hilft. Die Blickrichtung des Kapitäns erfolgt tangential zur Erdoberfläche. Damit ist ein rechter Winkel vorhanden und der Pythagoras kann genutzt werden. Erdradius und die gesuchte Sichtweite sind die Katheten eines rechtwinkligen Dreiecks. Die Hypotenus ist um 25 m länger als der Erdradius.
Mache als erstes eine (nicht maßstabsgetreue) Planskizze. D.h. schlage einen großen Kreis (r ~ 10cm) und zeichne senkrecht darauf die Höhe der Schiffsbrücke ein (h ~ 1cm). Nun zeichne die Sichtline, also die Linie von der Spitze der Schiffsbrücke ein welche den Kreis genau tangiert. Trage alle benannten und unbekannten Größen ein (in Metern, nicht in km!).
Dann rechne wie hier
https://de.wikipedia.org/wiki/Sichtweite#Geod%C3%A4tische_Sichtweite
Du malst einen Kreis. Das ist die "aufgeschnittene" Erde mit Radius (Mittelpunkt M zu Kreislinie) 6371 km.
Du malst eine Linie vom Mittelpunkt nach oben und verlängerst sie um 25m
Maßstabgsgetreu geht das nicht, also mach es einfach als Skizze.
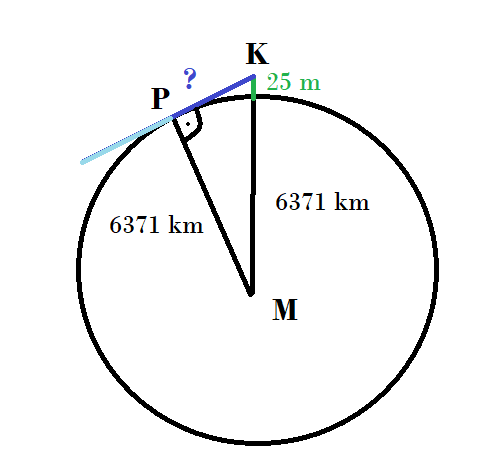
Oben auf der Linie, 25m über der Oberfläche/ dem Wasser und 6371,025km vom Mittelpunkt M entfernt, sitzt der Kapitän an Punkt K und kann von da bis zu dem Punkt P schauen, an dem sein Blick (gerade Linie) die Erdkugel gerade noch streift.
Dieser Punkt P liegt natürlich auf der Erdoberfläche und ist entsprechend r = 6371km vom Erdmittelpunkt M entfernt. Weil die Blicklinie eine Tangente ist (die Erde nur in diesem einen Punkt berührt), ist ihr Winkel zum Radius am Berührungspunkt P 90°.
Damit hast du ein rechtwinkliges Dreieck MKP, von dem du zwei Seiten kennst.
Der Rest ist Pythagoras.