Mathe: Winkel im Würfel
Wie berechnet man in einem Würfel mit der Seitenlänge a den Winkel zwischen den 2 Raumdiagonalen? Bisher habe ich nur die Länge der Diagonalen.
5 Antworten
Ich hab dir mal eine Zeichnung gemacht. Dort siehst du eine Hilfsfläche, auf denen sich die Raumdiagonalen befinden. Für den Winkel hast du ein gleichschenkliges Dreieck. In dem kannst du die Höhe einzeichnen, dann hast du 2 gleiche rechtwinklige Dreiecke. Diese ist ja genau die halbe Kantenlänge des Würfels. Damit kannst du den Winkel berechnen.
Ich komme auf 109,47°. Ich hoffe, ich hab mich nicht verrechnet.
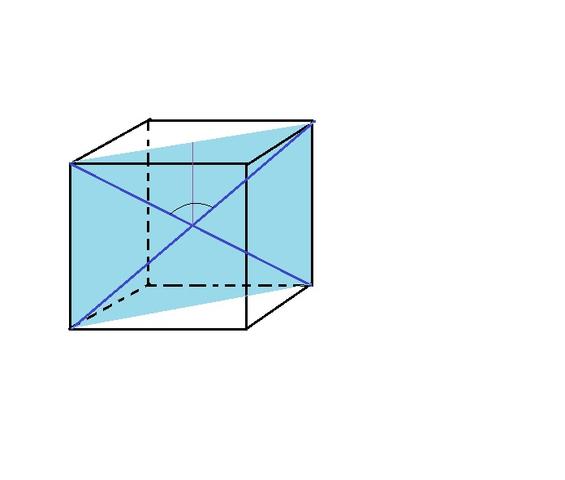
nachdem dort stand, dass man die höhe einzeichnen muss schon :D das rechnen habe ich dann selber gemacht ;D
Ein Kosinussatz für ein gleichschenkliges Dreieck mit zwei Seiten d' und eine weitere Seite a nimmt eine einfache Form an:
a² = d' ² +d' ² -2d' ²cos(φ) = d' ² (2 - 2cos(φ))
Also rechne ich analog Ellejolka mit der halben Raumdiagonale d' = (a√3)/2 , die dritte Dreiecksseite ist allerdings eine Würfelkante. Denn unter dem gesuchten Winkel für ich von einem Paar (Winkel, Nebenwinkel) den kleineren verstehen.
( (a√3)/2 )² * (2 -2cos(φ)) = a²; | * 4/(3a²)
2 - 2cos(φ) = 4/3;
cos(φ) = 1/3; φ = 70,53°
...passt (ist der Nebenwinkel des bereits gefundenen).
Skizze und mit Kosinussatz im Dreieck halbe Raumdiagonale, halbe Raumdiagonale, Flächendiagonale als Seiten.
Ich habe mal eine Skizze gemacht, aber es ist nirgends ein Winkel von 90 grad. Den Kosinussatz darf man doch nur bei rechtwinkligen Dreiecken anwenden, oder?
a = (1 1 1)
b = (-1 -1 1)
Inneres Produkt:
a * b = |a| * |b| * cos(a,b)
cos(a,b) = (a * b)/(|a| * |b|) = -1 -1 + 1/(Wurzel(3) * Wurzel(3)) = -1/Wurzel(3*3) = -1/3
Winkel(a,b) = arcos(-1/3) = 109,47°
wenn es sich tatsächlich um einen würfel handelt, dann schneiden sich die DREI Raumdiagonalen im Winkel von 90°
Nee, wenn du den Würfel schräg aufschneiden würdest, dann hättest du die Ebene auf der zwei Raumdiagonalen liegen. Und das ergibt aber ein Rechteck. Wenn du in einem Rechteck die Diagonalen ziehst, dann sind sie nicht rechtwinklig zu einander
Haste nich, Hut ab! (Bezieht sich auf verrechnet...)