Mathe trigonometrische Funktionen? Kurvendisskussion?
Bei der Aufgabe mussten wir die Nullstellen der trigonometrischen Funktion herausbekommen. Aber wie kommt man auf den Bereich und die Stellen?

2 Antworten
Hallo,
wie ist deine Funktion denn definiert? Also auf welchem Bereich? Den ganzen reellen Zahlen?
Dein Foto ist leider zu klein um es (ohne große Mühe) zu lesen.
Du hast die Funktionsgleichung:
f(x)=sin(2x)+3x angegeben.
Der Sinus kann nur Werte von -1 bis 1 annehmen.
Das heißt, dass eine Nullstelle nur in einem recht kleinen Bereich liegen kann. Denn 3x wird zu schnell 'groß'.
Wir haben ja de Worstcase 3x-1=0 und im besten Fall 3x+1=0
So kannst du den Bereich der Nullstelle eingrenzen. Die Nullstelle liegt also im Bereich [-1/3 , 1/3].
Eine algebraische Lösung für diese Gleichung gibt es nicht.
Du kannst sie nur numerisch lösen. Etwa mit dem Newton-Verfahren, falls ihr das in der Schule gelernt habt.
Tatsächlich ist es hier aber so, dass man die Nullstelle praktisch sofort sieht.
Nämlich x=0.
Es bleibt zu begründen, dass dies die einzige ist. Dafür könntest du zeigen, dass die erste Ableitung strikt positiv ist. Daher, die Funktion steigt immer.
Damit wäre gezeigt, dass deine Funktion eine sog. injektive Funktion ist.
Also wieso 3x+1=0, woher kommt die 1?
Weil der Sinus durch -1 und 1 beschränkt ist. Das heißt, dass man die Funktion
sin(2x)+3x 'zwischen' sin(2x)+1 und 'sin(2x)-1' einschließen kann.
Hier ein kurzes Bild zum Kommentar:
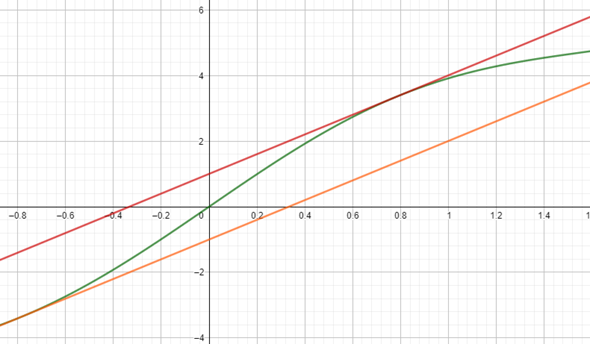
Grün ist sin(2x)+3x
Rot ist 1+3x
Orange -1+3x
Es handelt sich hierbei um Abschätzungen, um die Funktion sin(2x)+3x zu nähern.

Entschuldigung beim hochladen des Fotos wurde die Qualität stark beeinträchtigt. Also tatsächlich war die die Funktion ohne garnichts vorgegeben. Wie kommt man dann überhaupt auf die 1/3?