Mathe ln-Funktion Parameter?
Welches Einfluss hat jeder einzelne Parameter auf die Funktion?
f(x)=a*ln(bx^2+c)+d
2 Antworten
Es gibt mehrere Schaubilder, wie der Graph abhängig von a, b, c und d aussehen kann. Ich habe sie dir unten mal alle angehängt und gehe mal kurz darauf ein. Da d nur vertikal verschiebt, lasse ich diesen Parameter mal außen vor.
- a ∈ IR, b ≥ 0, c ∈ IR
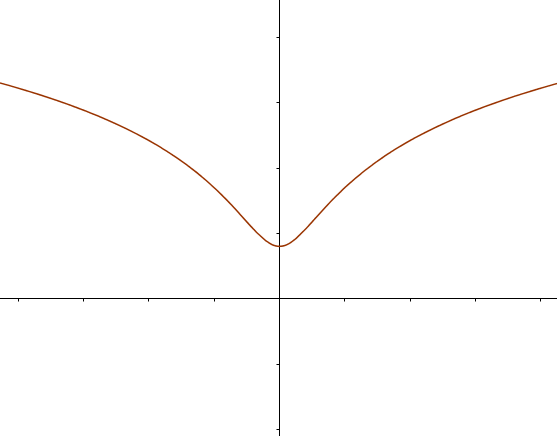
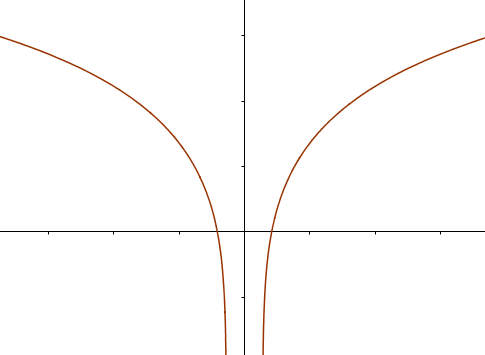
Für a = 0 und/oder b = 0 entspricht der Graph einer konstanten Funktion, für a ≠ 0 gleicht der Graph in etwa zwei an der y-Achse gespiegelten Logarithmusfunktionen, die abhängig von c in der Mitte stetig verbunden werden oder nicht (siehe Bild 1 und 2). a hat etwa den Effekt wie ihn ein Öffnungsfaktor bei einer Parabel hat (stauchen/strecken, spiegeln) und verschiebt zudem vertikal.
Für c ≤ 0 existiert eine Definitionslücke bei x = 0 und die beiden Graphstücke sind nicht mehr verbunden (siehe Bild 2), für c > 0 sind die beiden Graphstücke verbunden und auf der y-Achse existiert ein Extremum (siehe Bild 1).
b hat wie a Einfluss auf Streckung und Stauchung, verschiebt aber den Graphen nicht.
- a ∈ IR, b < 0, c ∈ IR
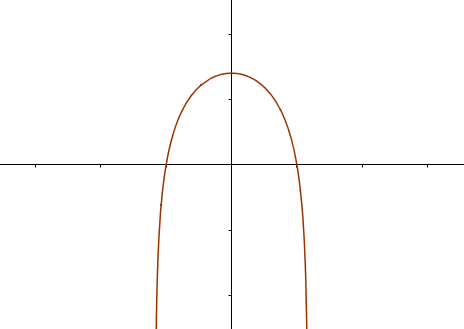
Für b < 0 existiert in jedem Fall ein Hochpunkt auf der y-Achse und der Graph hat ungefähr die Form einer nach unten geöffneten Parabel (siehe Bild 3). Er hat wie im obigen Fall Einfluss auf Stauchung und Streckung.
Für b, c < 0 ist die Funktion undefiniert (negativer Wert im ln).
c vergrößert/verkleinert den Graphen horizontal und vertikal und verschiebt vertikal.
a spiegelt an der x-Achse und flacht den null-nahen Teil ab.
LG Willibergi
Hmm ; schwierig . d ist ein y-Offset . Dann hast du noch die Identität
a ln ( u ) = ln ( u ^ a ) ( 1 )
b und c lässt sich nur schwer abschätzen. Weil du hast ja eine Kettenfunktion; du wendest einen Logaritmus auf eine Parabel an .
Wäre hilfreich, wenn du in ganzen Sätzen sprechen könntest .
bitte was? :(