Kurve in Polarkoordinaten?
Ich soll die Kurve
𝑟(𝜙)=cos(2𝜙)
im Polarkoordinatensystem skizzieren.
Bisher habe ich folgendes:

das scheint mir aber nicht richtig zu sein. Was mache ich falsch?
2 Antworten
Die Wertetabelle passt soweit.
Was ich mich jedoch Frage: Warum hast du bei 8π/6 aufgehört, anstatt bis 12π/6 (=2π) weiterzurechnen, damit du eine volle Periode hast?
============
Du hast dann jedoch nicht alle Punkte ins Koordinatensystem übertragen. So sehe ich beispielsweise den Punkt (r; φ) = (-1/2; 2π/6) nicht eingezeichnet.
============
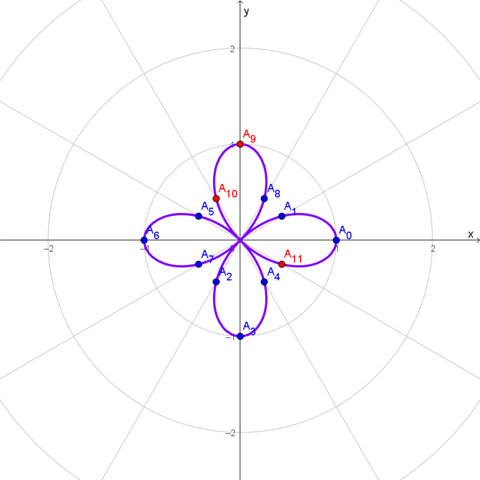
Hier mal zum Vergleich...

Da habe ich die von dir berechneten Punkte
- A₀ mit (r; φ) = (1; 0π/6)
- A₁ mit (r; φ) = (1/2; 1π/6)
- A₂ mit (r; φ) = (-1/2; 2π/6)
- A₃ mit (r; φ) = (-1; 3π/6)
- A₄ mit (r; φ) = (-1/2; 4π/6)
- A₅ mit (r; φ) = (1/2; 5π/6)
- A₆ mit (r; φ) = (1; 6π/6)
- A₇ mit (r; φ) = (1/2; 7π/6)
- A₈ mit (r; φ) = (-1/2; 8π/6)
in blauer Farbe und die Punkte
- A₉ mit (r; φ) = (-1; 9π/6)
- A₁₀ mit (r; φ) = (-1/2; 10π/6)
- A₁₁ mit (r; φ) = (1/2; 11π/6)
in roter Farbe und die Kurve in violetter Farbe eingezeichnet.
Vielen Dank für deine sehr ausführliche Hilfe : ) Du bekommst den Stern ; ))
Ja, genau. Negativer Radius bedeutet, dass die Punkte im Vergleich zu entsprechendem positivem Radius dann gespiegelt auf der anderen Seite bzgl. dem Ursprung liegen.
Wie hast du im Übrigen in Geogebra die Kurve auf Polarkoordinaten umgestellt? Ich kriege es nur hin, die Grafik auf Polarkoordinaten umzustellen.
Wenn du bei Punkten die Koordinaten mit Strichpunkt „;“ voneinander trennst, so interpretiert GeoGebra das als Polarkoordinaten.
(r; φ) wird dann als Punkt in Polarkoordinaten mit Radius-Koordinate r und Winkel-Koordinate φ interpretiert.
Um die Kurve zeichnen zu lassen, kann man dann dementsprechend beispielsweise [wenn GeoGebra auf Englisch gestellt ist]...
Curve((cos(2φ); φ), φ, 0, 2π)
... bzw. [wenn GeoGebra auf Deutsch gestellt ist]...
Kurve((cos(2φ); φ), φ, 0, 2π)
... eingeben.
Alternativ kann man auch manuell die Polarkoordinaten (r; φ) als kartesische Koordinaten (r * cos(φ), r * sin(φ)) umschreiben und dann dementsprechend [wenn GeoGebra auf Englisch gestellt ist]...
Curve(cos(2φ) * cos(φ), cos(2φ) * sin(φ), φ, 0, 2π)
... bzw. [wenn GeoGebra auf Deutsch gestellt ist]...
Kurve(cos(2φ) * cos(φ), cos(2φ) * sin(φ), φ, 0, 2π)
... eingeben.
Das Ding ist, dass ich meinte, ich müsste alle Punkte direkt verbinden. Daraus habe ich dann eine quadratartige Figur bekommen...Wie weiss ich "wie ich die Punkte verbinden soll"?
Naja. Direktes verbinden ist falsch. Die Punkte, die du berechnet hast, sind ja nicht die einzigen Punkte. Zwischen A₀ mit (r; φ) = (1; 0) und A₁ mit (r; φ) = (1/2; π/6) kann man ja beispielsweise den Zwischenpunkt (r; φ) = (√(3)/2; π/12) für den Winkel π/12 zwischen 0 und π/6 betrachten. Und dieser Zwischenpunkt liegt dann nun einmal nicht auf der direkten (geraden) Verbindungsstrecke zwischen A₀ und A₁.
Du solltest dir überlegen, wie die Kurve da [entsprechend abgerundet] durch die Punkte verlaufen könnte. Und wenn dir das zu schwer fällt... Dann musst du deinen Mangel an Vorstellungsvermögen durch Rechenaufwand ausgleichen und eben mehr Zwischenpunkte berechnen.
Wenn du die restlichen noch einzeichnest, sieht es doch ganz gut aus. So sollte es aussehen:


Ausserdem sind doch ein paar Radien negativ, soll ich diese dann einfach am Ursprung spiegeln?