Kugel Quader Volumen bei gleicher Oberfläche?
Wieso gilt, dass ein Würfel und eine Kugel mit gleichem Volumen einen solchen oberflächeninhalt haben, dass der vom Würfel größer ist als der von der Kugel? Ich kann es berechnen, ich würde es nur gerne qualitativ verstehen.
7 Antworten
Gehen wir mal andersrum an die Sache ran und betrachten die Oberfläche bei gleichem Volumen. Würden wir eine Kugekl und einen Würfel mit gleichem Volumen ineinander legen, würde die Kugel etwas über die Seitenflächen des Würfels hinausragen und die Ecken des Würfels würden aus der Kugel herausragen.
Die Kugel würde an 6 Stellen über die Flächen des Würfels ragen, aber 8 Ecken des Würfels würden aus der Kugel herausragen. Die Volumina der 6 Kugelabschnitte wären so groß wie die Volumina der 8 Würfelecken.
Nun kann man sich gut vorstellen, dass die Oberflächen, die die 6 Kugelabschnitte begrenzen in der Summe etwas kleiner sind als die 8 pyramidenartigen Eckflächen der 8 Würfelcken. Diese Differenz zwischen beiden macht die Würfeloberfläche größer als die Kugeloberfläche bei gleichem Volumen.
Andere Betrachtung: auf einem Bogen hat man immer eine kürzere Verbindung zwischen zwei Punkten als wenn man um die Ecke läuft.
Es ist eine allgemeine Erkenntnis, die man drauf haben sollte, weil sie öfters mal in der Natur auftritt: Kreis und Kugel gelten als ideale geometrische Körper, da es keine anderen Körper gibt, die im Verhältnis zur Fläche bzw. zum Volumen einen so geringen Umfang bzw. Oberfläche haben.
Okay, aber wieso läuft man länger um die Ecke?
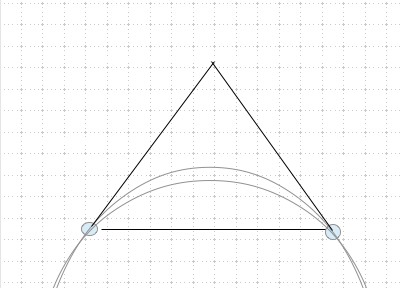
Grundsätzlich gilt: die kürzeste Verbindung zwischen zwei Punkten ist eine Gerade (unterste Kurve). Wenn man einen Bogen läuft, wird der Weg umso länger, je größer der Bogen ist. Noch viel länger wird der Weg, wenn man um eine Ecke läuft (Kurve ganz oben). Es nimmt zwar auch die Fläche zu, die man mit einem längeren Weg einschließt, aber die Flächenzunahme hinkt immer etwas hinter der Wegzunahme hinterher. Unter dem oberen Kreisbogen befindet sich etwa die Hälfte der Fläche gegenüber dem Dreieck. Der Weg um die Ecke (also entsprechend des Dreiecks) hat aber um mehr als das Doppelte zugenommen. Letztlich landen wir wieder bei dem Grundsatz: Bei einem Kreis ist das Verhältnis zwischen Fläche und Umfang maximal. Es gibt keine geometrische Figur, die ein besseres Verhältnis hat. Das lässt sich dann auch auf eine Kugel übertragen.
Ergänzung 2:
So sieht das aus, wenn der Würfel und die Kugel das selbe Volumen haben (258 cm^3)

Die Kalotten der Kugel, die über die Flächen des Würfels hinausragen haben dasselbe Volumen wie die Teile des Würfels am Rand, die von der Kugel nicht ausgefüllt sind.
Ich denke, da kann man mit etwas Fantasie durchaus erkennen, dass die blauen Oberflächen, die aus dem Würfel herausragen insgesamt kleiner sind, als die grünen Flächen ringsrum um die herausragenden Kalotten. Der Unterschied ist zwar nicht groß, aber er ist da. Hier noch die direkte Draufsicht:



Du kannst die meisten dieser Überlegungen auf die Ebene projizieren. Vielleicht hilft dir dieser Link zur Veranschaulichung:
Vielen Dank, wieso aber hinkt die Flächenzunahme?
Das ist halt so und lässt sich rechnerisch nachweisen. Ansonsten musst du die Erfinder von Kugel und Würfel fragen, was sie sich dabei gedacht haben.
Und wieso kann ich dieses Beispiel auf 3d übertragen?
Würfel und Kugel sind die Erweiterungen von Quadrat und Kreis in die dritte Dimension hinein.
Bei einem Kreis ist logisch, wenn ich ihn drehe, dass sodass wie ne Kugel entsteht, aber wenn ich EIN Quadrat um ein Punkt rotiere, kommt doch ein zylinder raus?
Für einen Kreis ist die natürliche Bewegung in die 3. Dimension selbstverständlich wieder eine Kreisbewegung, also eine Rotation.
Für ein Quadrat, das bereits die zwei Dimensionen definiert, ist die natürliche Bewegung eine translatorische Verschiebung in die 3. Dimension.
Aber dann kann man sie doch nicht vergleichen?
Und wieso nicht. Du hast doch schon den Beweis, dass man die Oberflächen bzw. Volumina miteinander vergleichen kann.
Ansonsten hat das Problem, was Kreis und Quadrat miteinander zu tun haben, die Mathematiker und schlausten Köpfe jahrhundertelang schwer beschäftigt. Dieses Problem nennt sich die Quadratur des Kreises und dieses Problem ist nicht lösbar, wie man heute weiß. Der Teufel, der hier im Detail steckt und die Lösung verhindert, nennt sich Pi.
Meine Fragen:
1. Wieso hinkt die Fläxhenzunahme?
2. Wieso kann ich durch diesen Vergleich der Flache auf den halt der Körper schließen?
Und wieso ist nicht der Ausschnitt aus dem die Kugel rausragt deutlich großer als die 8 Ecken des Würfel
Und wieso ist nicht der Ausschnitt aus dem die Kugel rausragt deutlich großer als die 8 Ecken des Würfel
Sonst hätte man am Ende keine gleichen Volumina.
1. Wieso hinkt die Fläxhenzunahme?
Das ist so. Wenn du es nicht glaubst, rechne es dir aus.
2. Wieso kann ich durch diesen Vergleich der Flache auf den halt der Körper schließen?
Das kannst du nicht, aber du kannst das Prinzip erkennen, dass gleichgroße Flächen mit unterschiedlichen Formen unterschiedliche Umfänge haben können und dieses Prinzip gilt auch im Raum. Da eben betreffs Volumen und Oberfläche.
Aber wieso ist die Oberfläche der 6 deutlich kleiner als die der 8 und wieso gilt das auch im 3d Raum
Manche Sachen in der Mathematik und der Physik muss man einfach so hinnehmen und sie akzeptieren, auch wenn sich der "gesunde Menschenverstand" irgendwie dagegen wehrt.
Ich erinnere mich noch gut an die Vorlesung zur Mechanik an der Uni, als der Professor die Kreiselgesetze und das Prinzip der Drehimpulserhaltung in Experimenten demonstrierte. Worum es da geht, kannst du hier sehen:
https://www.youtube.com/watch?v=GeyDf4ooPdo
https://www.youtube.com/watch?v=NeXIV-wMVUk
https://www.youtube.com/watch?v=GTk6GjQNd04
Anschließend meinte er singemäß: "Ich kann Ihnen versichern, dass ich die Kreiselgesetze rauf und runterrechnen kann, selbst wenn sie mich mitten in der Nacht wecken würden. Trotzdem wundere ich mich jedesmal, dass die auch in der Praxis so verblüffend funktionieren."
Wieso aber betrifft auch die Volumina? Ich möchte gerne verstehen
Vielleicht, um dir nochmal zu demonstrieren, was mein Problem ist:
Wie bei Finsterladen, stört mich diese Fläche, die über der des Quadrates eingenommen wird. Also wieso ist der Kreisweg dort kürzer als der innere liegende vom Quadrat?
Dann wie kann man dein Beispiel auf die 6 Stellen übertragen? Vielleicht habe ich nicht mitbekommen, was deine Zeichnung versucht zu sagen, aber ich sehe den Zusammenhang zu den 6Stellen, die aus dem "gemeinsamen" Volumen herausragen.
Leider habe ich gerade kein 3D-Bild einer eingeschriebenen Kugel da. Aber da kommt mit gerade eine Idee....
Ich kann es leider nicht erkennen, kannst du vielleicht einzeichnen, wie du es meinst, beziehungsweise woran man erkennt, dass die Fläche des umrahmenden Würfels größer ist?
Könntest du mal zeigen, dass die Flächen gl. groß sind?
Was ich nicht verstehe, wie kann man auf die Oberfläche schließen: wir sehen doch hier nur die kugel von außen und was ist mit der inneren oberfläche?
Ich kann es leider nicht erkennen, kannst du vielleicht einzeichnen,
Nein, das gibt das Programm nicht her. Wenn du es nicht glaubst, dann rechne es doch aus und schon ist alles klar.
Volumen Kugel:
V = 4/3 π r³
Volumen Würfel:
V = a³
Oberflächeninhalt Kugel:
O = 4πr²
Gleichheit Volumen:
4/3 π r³ = a³
Oberflächeninhalt Würfel:
O = 6a² <=> Oa = 6a³
<=> Oa = 6(4/3πr³) <=> O = 8πr³/a
Ungleichheit Oberflächeninhalt:
4πr² < 4πr² • 2r/a <=> 2r/a > 1 <=> r > a/2
<=> r³ > a³/8 = π/6 r³ <=> 1 > π/6
Das ist also für alle r und a wahr.
V = 4/3*pi*k^3 = w^3, also w = k * 1,612
mit k Kugelradius, w Würfelkantenlänge
Dann O_k = 4*pi*k^2 = 12,57k^2 und O_w = 6*w^2 = 15,6k^2
Interessante Frage, und vielleicht trifft es die Antwort von Wechselfreund am besten, man muss bei der Natur schauen. Das Nachrechnen ist nicht so schwer, die Interpretation des Ergebnisses schon eher. So geht es öfters mal in der Mathematik, dass man nicht so einfach eine intuitive Erklärung für ein Ergebnis parat hat.
Das kannst du doch einfach nachrechnen.
Berechne aus dem gegebenen Volumen zunächst Radius der Kugel bzw Seitenlänge des Würfels und daraus dann die jeweiligen Oberflächen. Dann siehst du es
Okay, aber wieso läuft man länger um die Ecke?Und wieso ist das Volumen der Außenecken größer als die der Kugel?