(Komplexe Zahlen, Pq Formel)Wie rechnet man für dieses Restpolynom die Nullstellen aus?

Wie berechnet man sowas mit der PQ Formel?

Man hat ja irgendwie trotzdem noch die j's übrig.

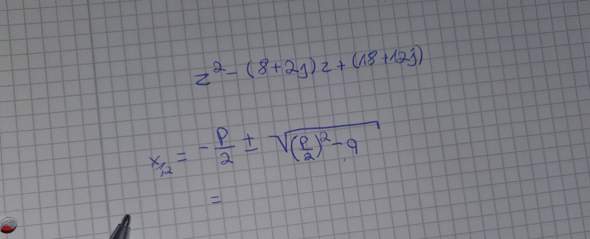
Bild zum Beitrag

J^2 ist=-1, aber wie sieht das bei dem Rest aus?

2 Antworten

Vom Fragesteller als hilfreich ausgezeichnet

Willy1729

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Schule, Mathematik

29.11.2020, 19:42

Hallo,

8+2j=p und 18+12j=q; -p/2=4+j

z1;2 ist also 4+j±√((4+j)²-18-12j).

(4+j)²=15+8j.

15+8j-18-12j=-3-4j.

Es ist die Wurzel aus (-3-4j) zu ziehen.

Dazu benötigst Du die Wurzel aus dem Betrag der Zahl, also die Wurzel aus √((-3)²+4²)=Wurzel aus √25=√5.

Dazu den arctan von -4/-3=233,13010235° (da die Zahl -3-4j im dritten Quadranten liegt, mußt Du zum Ergebnis 53,...° noch 180° addieren.

Da eine Wurzel von Grad 2 gezogen wird, teilst Du das noch durch 2 und kommst auf 116,5650512°.

Nun schreibst Du die Zahl in die trigonometrische Darstellung um und erhältst als die beiden Wurzeln von -3-4j √5*(cos (116,5650512°)+j*sin (116,5650512°))=-1+2j und √5*(cos (116,5650512°+180°)+j*sin (116,5650512°+180°))=1-2j.

Beide Wurzeln führen zu den beiden Lösungen 3+3j und 5-j für z.

Herzliche Grüße,

Willy

Loyaltinesswess

Fragesteller

29.11.2020, 19:57

Vielen Dank

Willy1729

03.12.2020, 13:41

Vielen Dank für den Stern.

Willy

Sophonisbe

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Mathematik

29.11.2020, 19:05

aber wie sieht das bei dem Rest aus?

Einsetzen und rechnen. Die binomischen Formeln werden nützlich sein.

Loyaltinesswess

Fragesteller

29.11.2020, 19:08

Ich hab echt keinen Plan wie das gehen soll, wenn da doch j's übrig bleiben würden

Loyaltinesswess

Fragesteller

29.11.2020, 19:19

Hello?

Sophonisbe

29.11.2020, 19:25

@Loyaltinesswess

Wieso so drängelnd?

setze die Terme für p und q ein, multipliziere aus und fasse zusammen.

Nach dem Abendessen bin ich dann vielleicht wieder online.

Loyaltinesswess

Fragesteller

29.11.2020, 19:53

@Sophonisbe

Sorry, war nicht böse gemeint

Hey Leute, wie berechnet man die Nullstelle dieser Funktionen ?? Danke im Voraus:-)

...zur Frage

Polynomdivision mit Rest die PQ-Formel?

Ich habe einen Polynom am dem ich die Polynomdivision angewand habe und schließlich die restlichen Nullstellen zu bestimmen.

f(x)=25³+15x²-9x+1

Die Nullstelle ich ich rausbekommen habe ist -1.

25x³+15x²-9x+1 / (x-0) = 25x²+15x-9 + (1)/(x-0)

Wie soll ich die Restlichen Nullstellen mit dem Rest berechnen?

...zur Frage

Quadratische Gleichungen mit PQ Formel Wie?

kann mir bitte jemand zeigen wie man es rechnet ich habe keine Ahnung wie ich die PQ Formel anwende !

vielen Dank

...zur Frage

PQ-Formel mit Eclipse?

Hallo,

ich hab versucht eine PQ-Formel zu erstellen:

        static final double pqFormeln(double a, double p, double q, boolean art) 
        {
                try 
                {
                  p/=a; q/=a;
                } catch (ArithmeticException e) 
                {
                  p/=-2;
                }
                double r = sqrt(p*p-q);
                if (isNaN(r))
                        throw new ArithmeticException("Keine reele Zahl. Lösung des "+(art?'+':'-')+" x Bereiches nicht möglich.");
                return art?p+r:p-r;
        }
        
        private static boolean isNaN(double r)
        {
                
                return false;
        }

        private static double sqrt(double d) 
           {
                return 0;
        }


}

Allerdings kann ich kein Java run machen. Meine Aufgabe lautet:

Wir wollen ein Programm schreiben, das die Nullstellen von quadratischen Funktionen der Form f(x) = x 2 + px + q berechnet. Die aus der Mathematik bekannte pq-Formel liefert uns die Nullstellen: x1,2 = − p 2 ± r p 2 4 − q Wenn der Term unter der Wurzel negativ ist, hat die Funktion keine (reelle) Nullstelle; ist er gleich 0, so gibt es genau eine Nullstelle. Schreiben Sie ein Programm PQ , welches p und q als Parameter ubergeben bekommt, die ¨ Nullstellen berechnet und ausgibt; geben Sie dabei zuerst die kleinere Nullstelle aus. Geben Sie anschließend aus, wie viele Nullstellen es gibt (Ausgabe nach dem Schema ” Es gibt 2 Nullstellen.“). Falls nicht genau 2 Argumente beim Programmaufruf angegeben werden, soll eine beliebige Fehlermeldung ausgegeben werden, die mit ERROR beginnt.

Kann mir jemand hier helfen?

...zur Frage

Betrag = Betrag, pq formel negative wurzel?

Welche reellen Zahlen x erfüllen folgende Gleichung:

| x^2 - 3x +6 | = | x-3 |

mir wurde das so erklärt, dass ich als aller erstes die Nullstellen vom linken und rechten Term ausrechne

links gibt es aber keine reellen Nullstellen, die Wurzel bei der PQ-Formel ist negativ

auf sowas hat man mich nicht vorbereitet, wie gehe ich jetzt weiter vor?

...zur Frage

Ab wann pq formel verwenden?

Wenn ich die Nullstellen von : f(x)=x^2-1 Berechnen soll, kann ich doch eigentlich

0=x^2-1 | +1 1=x^2 | ± √

x1 = √1 = 1 x2 = -√1 = -1

rechnen. Wofür bräuchte ich genau die pq formel? Bzw ist diese Aufgabe auch mit der pq formel zu lösen? Ich weiss das ich die pq formel bei zb. f(x)= x^2-2x+4 Verwenden muss:

x1,2=1±√(-2/2)^2-4

Ich bin mir jetzt nicht so sicher ab wann ich einfach wie oben "auflösen" darf und ab wann ich die pq formel verwenden muss

...zur Frage

Scheitelpunkt einer Parabel über PQ-Formel berechnen?!

Meine Frage: Ich habe eine normale quadratische funktion (x^2 + bx +c) und rechne mit der PQ-Formel jetzt die Nullstellen aus. Kann ich mit den Nullstellen dann auch den Scheitelpunkt ausrechnen oder muss ich die Quadratische Ergänzung benutzen?!

Ich hab in Erinnerung das es irgendwie auch mit den Nullstellen geht...

...zur Frage

Ist es möglich, unlösbare Gleichungen schnell zu erkennen (Beispiel mit PQ-Formel)?

Beim Lösen quadratischer Gleichungen stößt man manchmal auf Widersprüche, z.B. eine negative Diskriminante in der PQ-Lösungsformel. Rechnet man etwa die Nullstellen der Funktion f(x) = x^2 -4x +7 aus, ist im reellen Zahlenbereich spätestens ab 2 +/- sqrt(-3) Schluss.

Gibt es ein zuverlässiges Verfahren, welches solche unlösbaren Funktionen schnell enttarnt, das mühselige Ausrechnen erspart und auf alle Funktionen anwendbar ist?

...zur Frage

was bringt die pq formel und was bringt die quadratische ergänzung? wie findet man die nullstellen?

frage steht oben. wobei sollte man sie benutzen ?

und wie findet man die nullstellen, ganz am anfang ? einfach einsetzen uns ausprobieren ?

...zur Frage

PQ- Formel Domain Error?

Hey zusammen, ich habe ein Problem mit der PQ-Formel, mein Taschenrechner zeigt Domain Error an.

Die Aufgabe lautet: y = x²-2x-3

2 +/- √(-2/2)² - 3

Ich glaube das Ganze ist so, weil in der Wurzel ein negatives Ergebnis raus kommt,und ich glaube d. h. keine Nullstellen

Aber wie bekomme ich den aus

y = x²-2x-3 den Scheitel?

Ich dachte man müsste nur die Nullstellen rausfinden und dann in der Mitte zwischen diesen liegt der Scheitel

Würde mich sehr über Antworten freuen:)

...zur Frage

PQ-Formel auch bei Scheitelpunkt?

Hallo, ich schreibe morgen meine Matheklausur zum Thema Quadratische Funktionen und ich habe eine SEHR WICHTIGE Frage zum Thema PQ-Formel, ohne dessen Antwort ich WAHRSCHEINLICH EINE 6 schreiben werde.

Meine Frage:

Die Übungsaufgabe ist es, die Punkte P(?/?) und S(?/?) in die PQ Formel einzusetzen und dann die Nullstellen auszurechnen. Man darf jedoch nicht die Scheitelpunktform benutzen, obwohl der Punkt S ein Scheitelpunkt ist. Jetzt frage ich mich, ob man den Scheitelpunkt in der PQ-Formel genauso behandelt wie jeden anderen Punkt, oder ob es eine Extraregel gibt?

Bitte, bitte, bitte helft mir sonst schreib ich nh 5!!!!!
Danke!

...zur Frage

Pq-Formel Buchstaben statt zahlen?

Kann man bei der pq-Formel auch Buchstaben statt zahlen einsetzen,da wir das heute in der Mathestunde kurz besprochen haben,jedoch hab ich das nicht ganz verstanden.Könntet ihr Beispiele nennen?

danke schonmal

...zur Frage

Vielfachheit Nullstellen angeben?

Hallo, ich soll die Nullstellen der Funktion f(x) = x^3 + 8x^2 - x - 8 mithilfe der Polynomdivision und pq-Formel bestimmen.

Ich habe die Nullstellen 1, -1 und 8 raus.

Jetzt soll ich die Vielfachheit bestimmen. Wie mache ich das?
Wie bestimme ich den Schnittpunkt mit der y-Achse?

...zur Frage

Wie forme ich von der Scheitelpunktform auf die Normalpunktform um?

Ich schreibe Montag eine Mathearbeit und verstehe null.
Wie bringe ich den Scheitelpunktform in die Normalform und andersrum ?
Und wie bestimme ich die Nullstellen (PQ-Formel )?

...zur Frage

Was möchtest Du wissen?

Deine Frage stellen