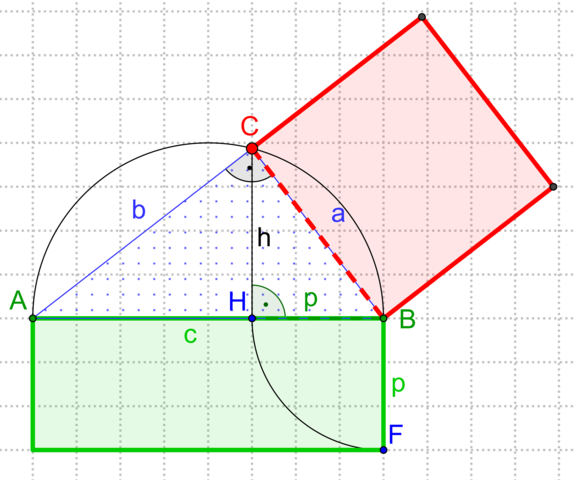
Kann mir jemand den Kathetensatz und den Höhensatz erklären?

Die Höhe auf die Hypotenuse teilt diese in 2 Abschnitte.

Der Kathetensatz stellt Beziehungen zwischen den Katheten und den Hypotenusenabschnitten dar.

Der Höhensatz stellt eine Beziehung zwischen der Höhe und den Hypotenusenabschnitten dar.

-----

Was fehlt dir zum Verständnis? Inhalt? Herleitung? Beweis? Bedeutung für den Rest der Geometrie?

Mit den Höhen im rechtwinkligen Dreieck ist es etwas seltsam.
Die Seite a ist die Höhe auf der Seite b und umgekehrt, weil sie im rechten Winkel aufeinanderstehen.

Die dritte Höhe ist das Lot von Punkt C zur gegenüberliegenden Hypotenuse c und steht im rechten Winkel auf c. Es reicht, wenn man sie h nennt.

Der Teil der Hypotenuse links von h  heißt q, der rechts davon p.
Merkwort: Coupé.

Das ist wichtig, denn jetzt liegt der Hypotenusenabschnitt p unter der Seite a und q unter b. (Sonst funktioniert der Kathetensatz nicht!).

Die jetzt folgenden Sätze von Euklid sind dem Satz von Pythagoras etwas ähnlich. Sie dürfen nicht verwechselt werden:

Kathetensatz (das sind 2, weil es ja zwei Katheten gibt):

a² =  c * p
b² =  c * q

Die alphabetische Reihenfolge    a vor b und  p vor q  ist ein Indiz für die richtige Anwendung.

Das Quadrat über einer Kathete ist gleich dem Produkt aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt.

Höhensatz

h² = p * q

Das Quadrat über der Höhe ist gleich dem Produkt der beiden Hypotenusenabschnitte.

Beide Sätze gelten nur im rechtwinkligen Dreieck.

---

Gegeben z.B. für den Höhensatz:

p = 4       q = 9
Dann ist   c = 13
              h² = 36
              h  =  6 

Mit dem Höhensatz kannst du sogar Wurzeln konstruieren!

Mal eine Herleitung (Höhensatz!).

Nehmen wir ein rechtwinkliges Dreieck und nennen es ABC. Nun teilen wir das rechtwinklige Dreieck in zwei rechtwinklige Dreiecke. Wir bekommen eine Höhe die h heißt.

Damit haben wir jetzt das Dreieck

AHC I ABC und HBC

Drücken wir mal die Dreiecke mit dem Satz des Pythagoras aus.

1) a^2 + b^2 = c^2
2) h^2 + p^2 = b^2 (In (I))
3) h^2 + q^2 = a^2 (In (I))

Noch was : Wegen der Höhe wurde die Hypotenuse Seite vom Dreieck ABC in zwei Hälften geteilt, sie werden p und q genannt, also gilt :

4)c = p + q (In (I))

So jetzt können wir herleiten.

Setze (III), (II) und (VI) in (I) ein.

(h^2 + q^2) + (h^2 + p^2) = (p+q)^2

h^2 + q^2 + h^2 + p^2 = p^2 + 2pq + q^2 I -p^2
h^2 + q^2 + h^2 = 2pq + q^2 I - q^2
2h^2 = 2pq I :2

—> h^2 = p * q

Das ist die Herleitung und man kann folgendes sagen :

Die Höhe vom Quadrat ist genauso groß wie das Rechteck p und q. Alles ein Verhältnis.

Für dich gilt : Wenn du mal p und q gegeben hast und h benötigst, wende diesen Satz an und stelle um.

Praktisch : Überprüfe kannst du auch damit, ob es sich um ein rechtwinkliges Dreieck handelt.

Tipp : Manchmal geht nichts, da kann es sein das du durch einsetzen die PQ Formel brauchst !

Ich lasse mal Bilder (für sich) sprechen...

links Kathetensatz, rechts Höhensatz

Reden sie deutlich genug? :-)