Kann einer diese Aufgabe erklären?
Kann einer die Nummer 2 schrittweise erklären kommen leider gar nicht mehr weiter
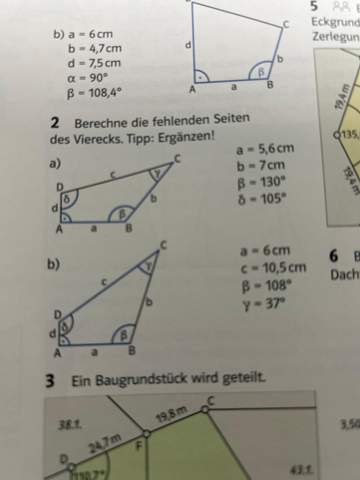
2 Antworten
zu 2a)
1) Winkel γ über die Winkelsumme im Viereck
2) Parallele zu AD durch B; Schnittpunkt mit DC ist E.
3) Winkel in Dreieck BCE sind 40°, 35° und 105°
4) BE und EC mittels Sinussatz in Dreieck BCE
5) Parallele zu AB durch D; Schnittpunkt mit BE ist F
6) DE mittels Kosinus in Dreieck DFE
7) EF mittels Tangens in Dreieck DFE
8) d = BE - EF
9) c = DE + EC
Die Winkelsumme im Viereck liefert den Einstieg, auch bei 2b).
Skizze:
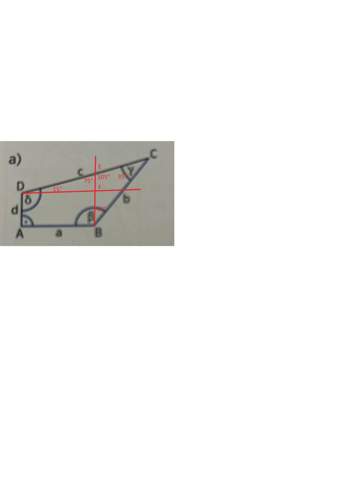
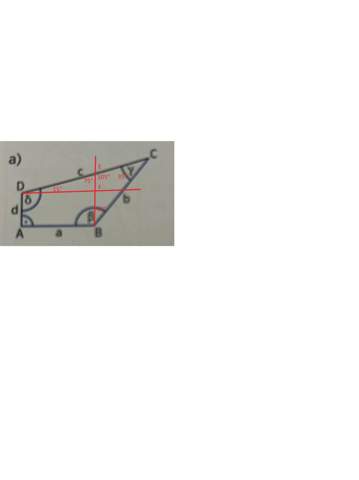
Kannst du eine Skizze machen habe es nicht so ganz verstanden
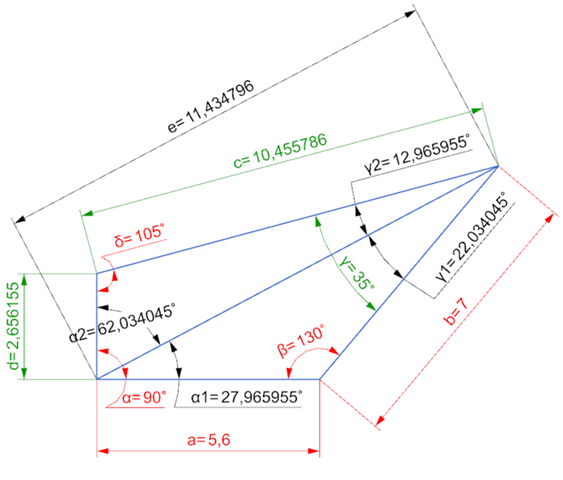
Aufgabe 2a
e = WURZEL( a² + b² - 2 * a * b * cos(β) )
e = WURZEL( 5,6² + 7² - 2 * 5,6 * 7 * cos(130) )
e = 11,434796 cm
---
α1 = ARCSIN( (b / ε) * sin(β) )
α1 = ARCSIN( (7 / 11,4348) * sin(130) )
α1 = 27,965955°
---
γ = 360 - α - β - δ
γ = 360 - 90 - 130 - 105
γ = 35°
---
γ1 = 180 - α1 - β
γ1 = 180 - 27,965955 - 130
γ1 = 22,034045°
---
γ2 = γ - γ1
γ2 = 35 - 22,034045
γ2 = 12,965955°
---
d = e / SIN(δ) * SIN(γ2)
d = 11,434796 / SIN(105) * SIN(12,96596)
d = 2,656155 cm
---
c = e / SIN(δ) * SIN(α2)
c = 11,434796 / SIN(105) * SIN(62,034045)
c = 10,455786 cm
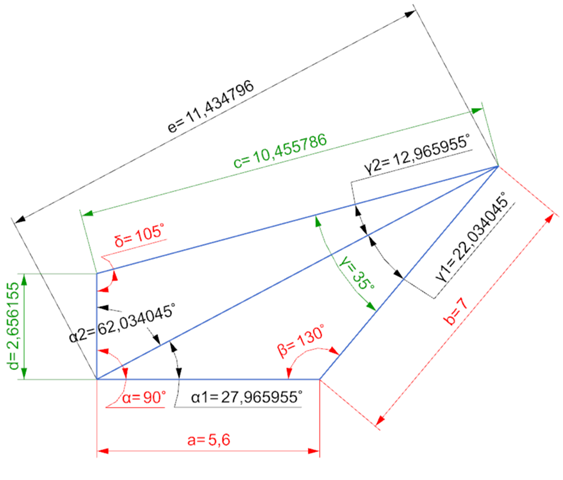
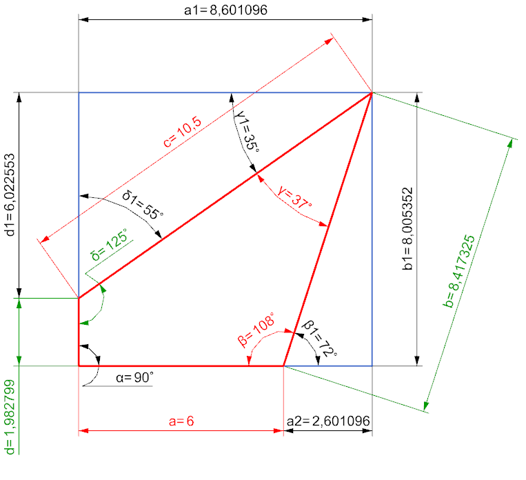
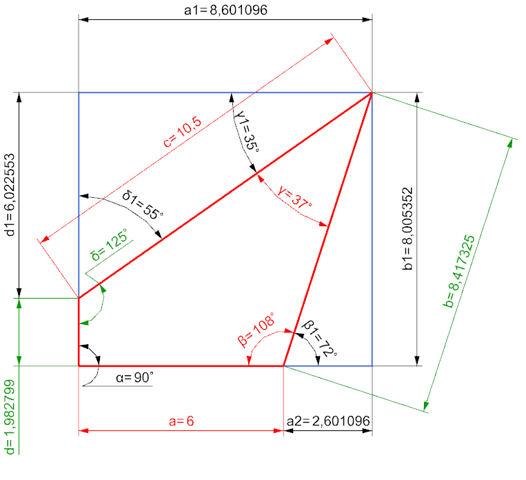
Aufgabe 2b
a1 = c * SIN(δ1)
a1 = 10,5 * SIN(55)
a1 = 8,601096 cm
---
d1 = c * COS(δ1)
d1 = 10,5 * COS(55)
d1 = 6,022553 cm
---
a2 = a1 - a
a2 = 8,601096 - 6
a2 = 2,601096 cm
---
b = a2 / COS(β1)
b = 2,601096 / COS(72)
b = 8,417325 cm
---
b1 = a2 * TAN(β1)
b1 = 2,601096 * TAN(72)
b1 = 8,005352 cm
---
d = b1 - d1
d = 8,005352 - 6,022553
d = 1,982799 cm