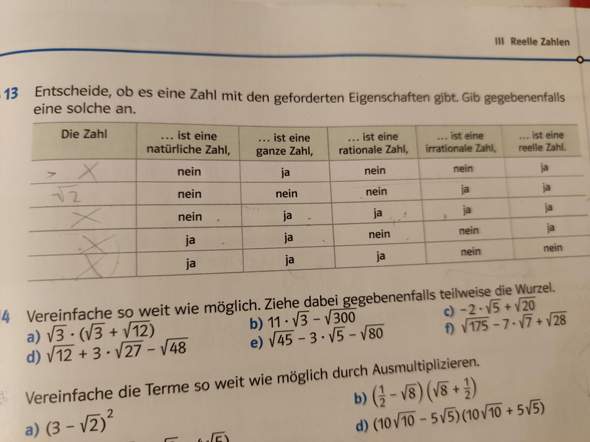
Kann eine Zahl gleichzeitig irrational und rational sein?
Also hier die Aufgabe:
Bei der 3 Zahl steht ja, dass sie irrational und rational ist. Ich dachte eigentlich, dass sowas nicht geht, da rationale Zahlen sind ja zahlen die man in ein Bruch umwandeln kann und irrationale zahlen sind zahlen die unendlich lang sind, (keine Periode!!) Und deswegen sich nicht in ein Bruch umwandeln können. Deswegen habe ich auch ein Kreuz dahin gemacht, aber im Buch steht, dass die Zahl -19 ist. Kann mir das jemand bitte erklären?Danke vielmals!!
Übrigens, bitte beachtet nicht, dass ich in mein Buch reingeschrieben habe, ich mache das öfters aber radiere das natürlich danach weg!!
2 Antworten
Nein, kann sie nicht.
Rational und irrational sind gegenseitig exklusiv.
Und wenn in diesem Buch tatsächlich steht, dass -19 sowohl rational als auch irrational sei, dann sollte derjenige, der für dieses Buch verantwortlich ist ganz dringend seinen Job entzogen bekommen und niemals wieder in die Nähe von irgendwelchen Büchern gelassen werden...
Nein, -19 ist keine irrationale Zahl, erfüllt die geforderten Eigenschaften also nicht. (Wenn in deinem Buch an dieser Stelle -19 steht, handelt es sich um einen Fehler.)
Es gibt keine Zahl, die zugleich rational und irrational ist. Denn irrationale Zahlen sind nach Definition genau diejenigen reellen Zahlen, die nicht rational sind.