Kann ein Halbkreisgraf eine Funktion sein?
Schließlich ist ja ein Kreisgraf keine Funktion. Also kann ein Halbkreisgraf auch keine sein. Richtig?
4 Antworten
Natürlich kann ein halber Kreis gezeichnet werden, da jedem x eindeutig ein y zugeordnet ist!
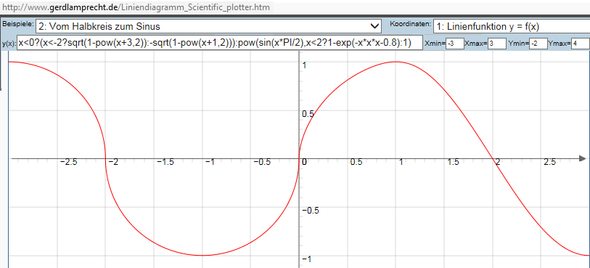
Unter http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
Beispiel 2 kann man 2 Halbkreise aneinanderheften und dann stufenlos in eine sin-Funktion übergehen...
siehe Bild
Wen das zu kompliziert ist, der fängt mit dem einfachsten Halbkreis an:
sqrt(1-pow(x,2)) = Wurzel( 1 - x² )
solange der Halbkreis die obere oder unter Hälfte ist schon, weil dann ist jedem x-Wert genau 1 y-Wert zugeordnet;
nimmst Du die linke oder rechte Kreishälfte hast Du keine Funktion
Ja dachte ich mir.. Also kommt es darauf an wie es gezeichnet ist. Danke dir❤️
Ein Kreisgraph ist keine Funktion, weil er jedem x-Wert zwei y-Werte zuordnet, also keinen Eindeutigkeit besteht (außer am jeweils äußersten linken und rechten Rand).
Wenn man aber von diesem zwei y-Werten jeweils einen "rausschmeißt", erhält man wieder Eindeutigkeit und damit eine Funktion - und wenn man z. B. immer den größeren Wert streicht, erhält man einen "unteren Halbkreis".
Also: Ein Halbkreis in beliebiger Lage ist auch nicht unbedingt eine Funktion, in "passender" Lage - nämlich als genau "oberer" oder "unterer" Halbkreis - aber schon.
Sin/Cos kurven sind aneinandergereiht halbkreise. Wenn du eine passende Parabel hast hast du auch einen Halbkreis. Also ja, das geht. Übrigens: Einen kreis kannst du schon als Graphen darstellen und zwar mit der Vektorendarstellung [X-M]^2=r^2.
Schau dir mal die genannten Funktionen genauer an. Halbkreise sind das bestimmt nicht.
Eine Sinusfunktion hat mit einem Halbkreis so ziemlich überhaupt nichts zu tun