Ist die Aussage "Wenn in einem Viereck die Diagonalen gleich lang sind, ist es ein Rechteck" falsch?
Ich mache gerade Mathe und hab keine Ahnung. Hoffe, jemand ist klüger als ich und weiß die Antwort...
Vielen Dank im Voraus ;-)
5 Antworten
Wenn man nicht mehr weiter weiß... dann nimmt man am besten ein Blatt Papier und kritzelt (Der Profi nennt das dann hochtrabend "Skizze")
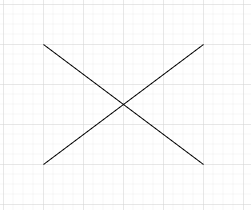
Zwei gleichlange Diagonalen...
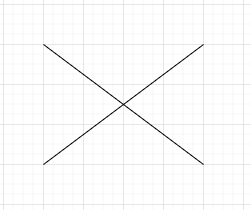
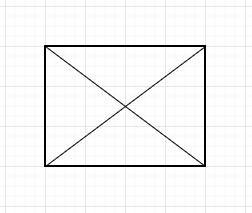
ergeben ein Rechteck:
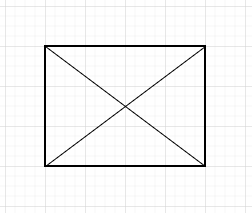
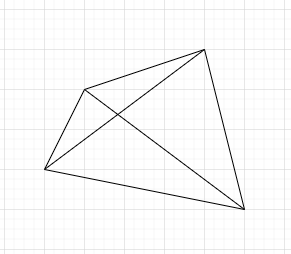
Ja super, dann stimmt die Ausage, oder? Aber was ist, wenn ich die Linien verschiebe?
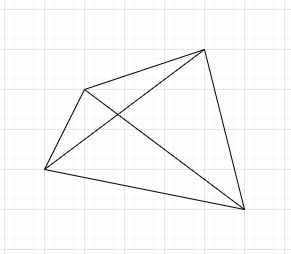
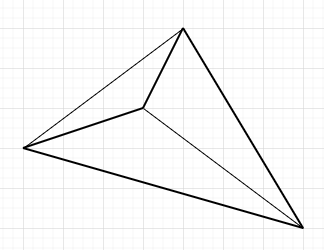
oder gar so:
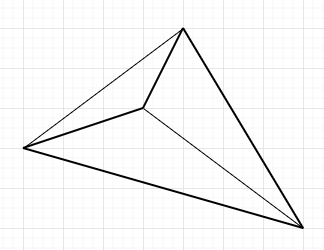
Deiner Aussage fehlt nämlich ein kleiner, aber wichtiger Teil:
"Wenn in einem Viereck die Diagonalen gleich lang sind und sich gegenseitig hablieren, dann ist es ein Rechteck"
Im Allgemeinen ist es kein Rechteck.
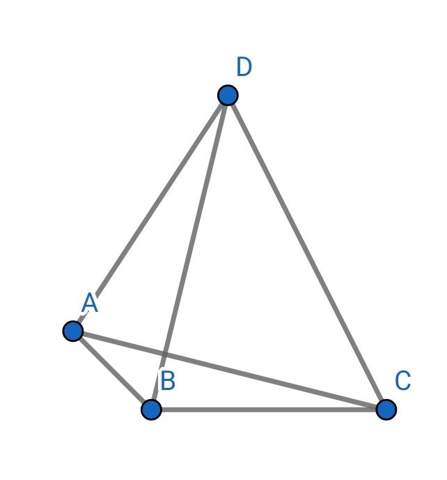
Ich habe ein bisschen mit Geogebra gespielt:
Die Diagonalen sind gleich lang. Es ist aber weder Rechteck noch Trapez. Ich bin mir nicht sicher, ob es überhaupt einen besonderen Namen hat.
Dass die Diagonalen anscheinend senkrecht auf einander stehen, ist keine Absicht.
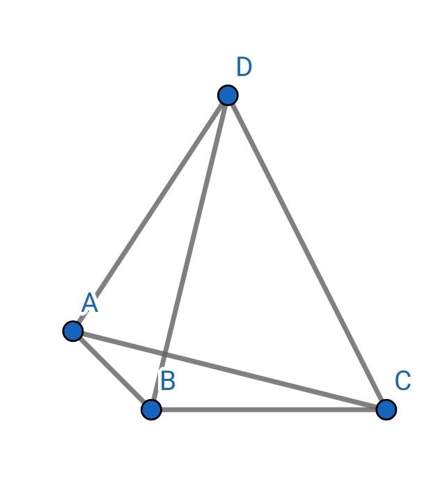
Die Aussage ist falsch.
Nimm einfach zwei Streichhöler und lege sie so übereinander, dass sie sich zwar kreuzen, aber nicht in der Mitte eines jeden Holzes. Dann verbinde die Enden der Hölzer zu einem Viereck. Dieses hat gleich lange Diagonalen (die Hölzer), ist aber bestimmt kein Rechteck.
Hallo,
Nein, das stimmt nur dann, wenn die gleich langen Diagonalen sich auch gegenseitig halbieren, also sozusagen genau in der Mitte treffen.
Die gleiche Länge haben sie auch bei solchen Vierecken:
https://www.mathebibel.de/gleichschenkliges-trapez#spezielle-eigenschaften
Nimm zwei gleich lange Bleistifte und probier es aus, indem du die Stifte gegeneinander bewegst.