Ist der Tunneleffekt schneller als Licht?
Ist der Tunneleffekt schneller als Licht?
4 Antworten
Der Tunneleffekt ermöglicht Teilchen das Durchdringen von Barrieren auf eine Weise, die klassisch nicht möglich wäre, aber er stellt keine Überschreitung der Lichtgeschwindigkeit dar oder ermöglicht eine Übertragung von Informationen schneller als das Licht.
Das ist eine gute Frage!
Ein Quantenobjekt (wie z.B. ein Elektron), wird mathematisch als eine Wellenfunktion beschrieben. Die Amplitude ("Stärke") dieser Wellenfunktion gibt an einer spezifischen Stelle die Wahrscheinlichkeit an, dass bei einer Messung das Teilchen dort gefunden wird.
Der Tunneleffekt ist nun die Tatsache, dass die Wellenfunktion bei einer Potentialbarriere (also irgend eine Form von Energiehinderniss wie z.B. die Coulomb Abstoßung eines anderen Atoms) innerhalb der Barriere nur exponentiell und eben nicht sofort abnimmt. Das bedeutet, dass das Teilchen eine gewisse Aufenthaltswahrscheinlichkeit innerhalb der Barriere hat, aber eben auch "dahinter". Wenn die Amplitude nämlich noch nicht auf null abgesunken ist, sobald die Barriere zu Ende ist, gibt es eine endliche Geschwindigkeit das Teilchen auch hinter der Barriere zu finden - selbst wenn die Energie, die für das Durchqueren der Barriere nötig ist größer wäre, als die Energie, die das Teilchen besitzt (was klassisch eigentlich verboten wäre).
Dann zu deiner Frage der Geschwindigkeit. Wo das Teilchen ist, kann man nicht so genau sagen, da ein "Teilchen" als Wellenpaket beschrieben wird. Das kann man sich so vorstellen:
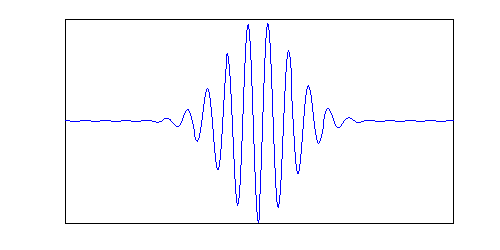
Dies erreicht man mathematisch, indem man viele einzelne Wellen mit unterschiedlicher Ausbreitungsgeschwindigkeiten überlagert. Quantenphysikalisch bedeutet das, dass dieses Teilchen mehrere Geschwindigkeiten gleichzeitig hat. Je schmaler das Teilchenpaket sein soll (also je genauer man den Ort kennen möchte), desto mehr unterschiedliche Geschwindigkeiten muss man überlagern. Mit anderen Worten: Je genauer man den Ort kennt, desto ungenauer wird die Geschwindigkeit. Dies gilt auch anders herum und ist als Heißenberg'sche Unschärferelation bekannt.
Das verkompliziert natürlich die Antwort auf deine Frage, denn damit gibt es nicht wirklich eine "Geschwindigkeit" des Teilchens, sondern nur eine Überlagerung. Allerdings sollte sich jede Welle einzeln nur mit maximal Lichtgeschwindigkeit ausbreiten können, weshalb es trotzdem nicht möglich sein kann, dass der Ort des Teilchens an unterschiedlichen Zeitpunkten als Überlichtgeschwindikgeit detektiert wird.
Also nochmal zusammengefasst: Nein, beim Tunneleffekt sollte dies nicht möglich sein. Anders (und etwas umstritten) sieht es beispielsweise bei der Quantenverschränkung aus ("spukhafte" Fernwirkung).
nein.
es gibt keine grund warum das so sein sollte und keinen hinweis darauf dass es so wäre.
Es gibt verschiedene Interpretationen dazu.
Die QM erlaubt eine entsprechende Geschwindigkeit (schneller als das Licht), weil die Ortsangabe unscharf ist. Und wenn ein Teilchen durch einen verbotenen Bereich tunnelt, erfogt das quasi instantan, da es nur eine Wahrscheinlichkeit für den Aufenthalt links oder rechts gibt, aber keine Wahrscheinlichkeit für den Aufenthalt in der Potential-Barriere.
Darüber gab es schon viele Diskussionen, ohne wirklich eindeutige Ergebnisse.
Am wahrscheinlichsten (meine subjektive Interpretation) ist, dass der Weg, den ein QM-Teilchen in einem verbotenen Bereich (z.B. Potentialbarriere) überwindet, aus QM-Sicht schlichtweg nicht als Weg zählt. Stattdessen gibt es eine Wahrscheinlichkeit dafür, dass das Teilchen links odder rechts von der Barriere angetroffen wird. Und ohne Weg gibt es kein Problem mit der SRT (Lichtgeschwindigkeit).
.
Andere Überlegung: Ist das wirklich relevant?
Tunneleffekt in der QM sind relativ selten (nicht prinzipiell, sondern bezogen auf die Anzahl der Teilchen, die wirklich tunneln) und nehmen mit der Breite der Barriere exponentiell ab.
Wenn es solche Überlichtgeschwindigkeitseffekte innerhalb eines Halbleiters mit Strukturbreiten von wenigen nm gibt, dann ist das gegen die sonstige Verarbeitungsgeschwindigkeit des Chips absolut nicht relevant.
Bei größeren Abständen, bei denen sich die Geschwindigkeitserhöhung gegenüber der Lichtgeschwindigkeit positiv auswirken würde, ist die exponentielle Abnahme des Signals so stark, dass man eigentlich nicht mehr von Signalübertragung sprechen kann.
Ergebnis:
Für alle wirklich relevanten Effekte (über relevante, zumindest etwas größere Entfernungen, > 1m) ist die Lichtgeschwindigkeit nach wie vor die absolute Grenze (Spezielle Relativitäts-Theorie).
Für QM-Effekte im wirklich molekularen Maßstab gelten dann die Regeln der QM und nicht die der SRT. Allerdings sind die dabei auftretenden Zeitgewinne so minimal, dass das keine relevante Rolle spielt.
==> Was ist also richtig?
Nach Allem was ich bisher weiß, schlägt die QM die SRT. Allerdings halt nur im "Streit um des Kaisers Bart", also in der Prinzipienfrage. In der Realität müssen wir auch weiterhin mit den Einschränkungen der SRT leben-
Ich verstehe was du meinst, aber es sollte doch trotzdem nicht möglich sein, zwei Ortsmessungen so zu konzipieren, dass die zeitliche und örtliche Differenz zu einer Überlichtgeschwindigkeit führt. Immerhin erzwingt eine Ortsmessung den Kollaps der Wellenfunktion und die natürlich Ausbreitung dieser Wellenfunktion erfolgt maximal mit Lichtgeschwindigkeit.