Hochpunkt, Tiefpunkt, Sattelpunkt berechnen?
Hallo Leute,
Bin gerade sehr verzweifelt, sitze seit 2 Stunden an diese Aufgabe. Habe sie im Taschenrechner berechnet und es war richtig. Aber ich möchte rechnerisch berechnen also f', f" und f'=0.
Hatte aber ganz andere Ergebnisse als im Taschenrechner. Und sie waren zudem alle falsch. 😕
Kann mir bitte erklären wie ich es rechnerisch lösen kann bitte?

2 Antworten
Hier schon mal von mir die Extrema:
f'(x)=3x²+12x+9=0
0=x²+4x+3
x1,2=-2±√(4-3)=-2±1
x1=-3, x2=-1
f"(x)=6x+12
f"(-3)=6(-3)+12=-18+12=-6<0 -> HP
f"(-1)=6(-1)+12=-6+12=6>0 -> TP
Graphisch kann man das bestätigen:
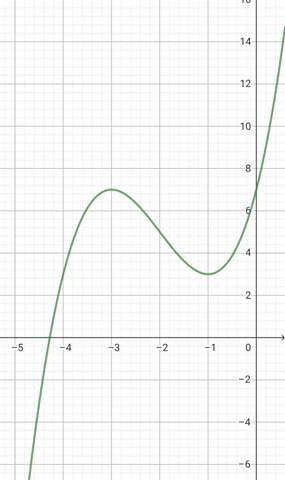
Nicht vergessen: Eine Stelle ist noch kein Punkt. Sattelstellen hat die Funktion nicht.
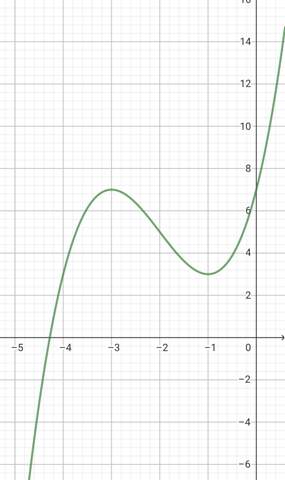
Also hab das gerade mit Pq Formel gemacht also so:
-4:2+- wuzel (x²:2)² - 3
Hab falsches Ergebnis raus bekommen.
Achso mit dem Vorzeichenwechsel habe ich gar nicht gemacht.
Vielen lieben Dank.
Um die Extrema davon als erster Schritt zu berechnen, musst Du zunächst die erste Ableuitung davon finden und dann deren Nullstellen finden.
Nullstellen : x^2 + 4x + 3, ie. x = -1 und x = -3
Nun finden wir die zweite Ableitung davon, welche die Ableitung der ersten Ableitung ist.
f''(x) = 6x + 12
Damit Du bestimmen kannst, welche die Hoch- und Tiefpunkte dieser Funktionen sind, solltest Du Dir überlegen, dass es ein Hochpunkt ist, wenn der Wert von f''(a) oder f''(b) mehr als 0 ist.
Im Gegensatz zu dem Hochpunkt hier ist der Wert des Tiefpunktes weniger als 0.
Wenn ich -3 und -1 in die Werte der zweiten Ableitung hinzufüge, bekomme ich dann die folgenden Ergebnisse :
f''(-3) = -6 ( Tiefpunkt ), f''(-1) = 6 ( Hochpunkt )
Aber wie bist du auf das gekommen?
0=x²+4x+3