Hilfe Vortrag Mathe Satz des Pythagoras Pyramide?
Moin Leute, ich muss am Montag einen Vortrag über Schnitte in einer Pyramide halten und wie man das mit dem Satz des Pythagoras berechnet. In meinem Vortrag will ich auch die wichtigsten Begriffe erklären, wie zum Beispiel Grundfläche, Seitenfläche, Mantelfläche, Höhe und so weiter. Ich brauche eine einfache und verständliche Erklärung, wie man solche Sachen berechnet und die Begriffe richtig benutzt. Könnten Sie mir das bitte Schritt für Schritt erklären, damit ich das gut rüberbringen kann? Danke im Voraus 👍🏻

3 Antworten
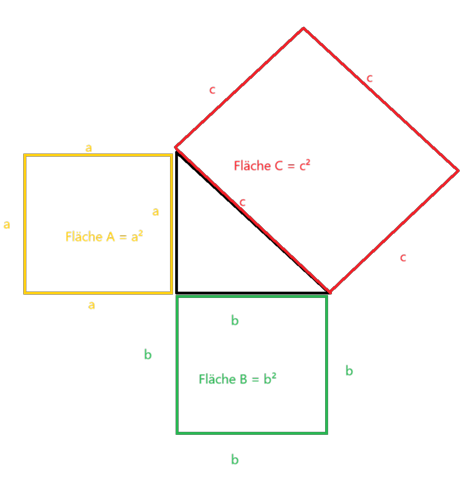
Der Satz des Pythagoras bezieht sich ausschließlich auf rechtwinklige Dreiecke, d. h. ein Innenwinkel beträgt 90°. Dieser Winkel liegt gegenüber der Seite c, die längste Seite des rechtwinkligen Dreiecks.
Der Satz besagt: a² + b² = c²
Im Grunde bedeutet das, dass die Summe der Flächen der beiden Quadrate mit 1) Seitenlänge a und Seitenlänge b) genau der Fläche des Quadrats mit der Seitenlänge c entspricht. Einmal grafisch... du denkst dir an jede Seite des Rechtsecks ein Quadrat und die Flächen aus A und B ergeben zusammenaddiert die Fläche von C.

Mit dieser Formel kannst du durch Umstellen also Flächen berechnen, aber auch die Länge einer fehlenden Seite.
Wenn zum Beispiel c nicht bekannt ist, jedoch a und b dann...
a² + b² = c² -->
Auf die Pyramide bezogen, mit Verweis auf mein Bild wie ich die Seiten beschrieben habe, scheint b die Hälfte einer Seite der Grundfläche der Pyramide zu sein.
Die Grundfläche der Pyramide scheint quadratisch,
d. h. eine Seitenlänge der Pyramidengrundfläche = 2 * b.
Der Flächeninhalt eines Quadrates berechnet sich mit A = Seitenlänge², also eine Seitenlänge zum Quadrat.
Damit kannst du auch die Fläche der Grundfläche der Pyramide berechnen, die da wäre: G = (2 * b)².
Die Seite a des rechtwinkligen Dreiecks aus der Zeichnung von mir kennzeichnet die Höhe der Pyramide.
Mantelfläche Pyramide:
Die Pyramide selbst hat an den Seiten 4 Dreiecke.
Eine dieser Seitenlängen ist bereits bei der Grundfläche der Pyramide berechnet worden: 2 * b bzw. es entspricht 2*b einer Seite der Grundfläche der Pyramide (Quadratische Fläche).
Die Höhe eines solchen Seitendreiecks entspricht c des rechtwinkligen Dreiecks.
Bei der Mantelfläche können wir jetzt nicht mit dem Satz des Pythagoras vorgehen, weil es sich nicht um ein rechtwinkliges Dreieck handelt.
Wir können lediglich eine berechnete Seite verwenden, nämlich c. Und die Seitenlänge 2*b.
Die Mantelfläche, also die Fläche der 4 gleichseitigen Dreiecke, berechnet sich mit
M = Seitenlänge * Höhe des Seitenstücks * 2
Eine Seitenlänge entspricht (wie oben berechnet) (2 * b).
Die Höhe des Seitenstücks entspricht c.
Damit berechnet sich unsere Mantelfläche: M = (2*b) * c * 2 = 4 * b * c
Die Fläche der Pyramide ergibt sich aus der Grundfläche G und der Mantelfläche M.
F = G + M
Vielleicht noch etwas - wie man sich die Fläche des Pyramidenmantels aus einem rechtwinkligen Dreieck herleiten kann:
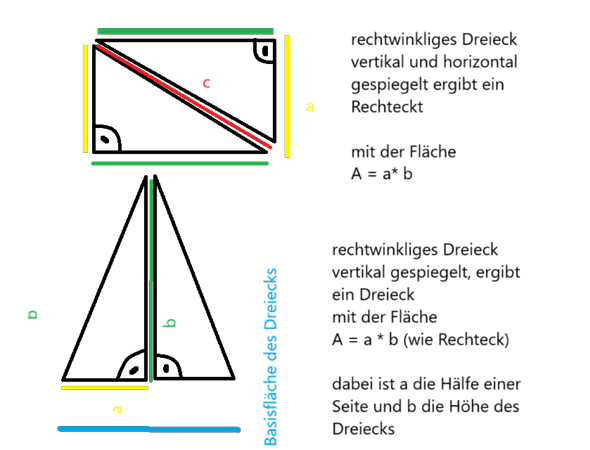
Das rechtwinklige Dreieck verdoppelst du und du erhältst ein Rechteck.
Die Fläche eines Rechtecks wird mit A = a * b berechnet, d. h. man multipliziert die Seitenlängen miteinander.
Du kannst aber die beiden rechtwinkligen Dreiecke auch so spiegeln und anordnen, dass ein Dreieck entsteht, ähnlich wie eine Mantelseite deiner Pyramide.
Mein unteres Beispiel zeigt das.
Ich habe das Dreieck außerdem gedreht, so dass es steht und nicht liegt... ist besser für die Ansicht.
Anhand der Farben gelb und grün siehst du, welche Seiten zu was gehören.
Die Fläche der Gesamtkonstruktion, also dem Dreieck, wird ebenso mit a * b berechnet.

Die Flächenberechnung des neuen Dreiecks können wir analog zur Flächenberechnung des Rechtecks durchführen: Es ist die gleiche Fläche, nur zerschnitten und anders angeordnet. ABER hier musst du beachten, dass bei der Flächenberechnung - ausgehend vom Rechteck - a nur die Hälfte der gesamten "Basis-Strecke" (hellblau) des Dreiecks ist. Hier dürfen wir nicht die Basisstrecke mit b multiplizieren, sondern nur die Hälfte der Basisstrecke, also a. Deswegen berechnet sich der Flächeninhalt eines Dreiecks mit
(Basisfläche wie im Bild ist vielleicht der falsche Ausdruck, Basis-Strecke trifft es besser)
entspricht damit also der gelben Linie a.
Damit hätten wir den Flächeninhalt eines Dreiecks. Da wir diese Formel aus der Flächenberechnung eines Rechtsecks abgeleitet haben, ist es völlig irrelevant, wie hoch das Dreieck ist oder wie lang die Basisstrecke ist. Ein Rechteck hat auch keine Einschränkungen. (Bei einem Quadrat sähe das anders aus, weil hier die Bedingung gilt, dass jede Seitenlänge gleich sein muss. Bei einem Rechteck ist das nicht der Fall.) Entsprechend kannst du das für alle Dreiecke anwenden... falls du mal die Formel vergessen hast... oder so.
Weiter geht's zur Mantelfläche...
Der Mantel besteht aus 4 Dreiecken. Das heißt, wir müssen 4 mal die Fläche des Dreiecks A rechnen:
Dann ziehen wir noch 4 und 1/2 zusammen...
, also...
2 * Basis des Dreiecks * Höhe des Dreiecks
--> das ist die gleiche Formel wie oben
M = Seitenlänge * Höhe des Seitenstücks * 2
Die Höhe entspricht in meiner Zeichnung b.
Die Seitenlänge entspricht der hellblauen "Basis-Linie des Dreiecks".
Du musst doch einfach den satz des pytagoras kennen und ihn anwenden können wenn nicht kann ich dir helfen (wenn du hilfe suchst fa)
Um das angegebene Dreieck zu berechnen brauchst du ganz allgemein den Satz des Pythagoras.
Du musst da ja immer Kathete (zum Quadrat) + Kathete (zum Quadrat) = Hypotenuse (zum Quadrat) rechnen.
Die Höhe ist deine eine Kathete und dann brauchst du die halbe grundseite also die,die unten an die Schrägseite angrenzt. Dann brauchst du nur noch die Seitenkanten ausrechnen.Das bekommst du raus wenn du die Seitenfläche hast und sie durch zwei nimmst,um nochmal Pythagoras anzuwenden und dann kannst du das alles ausrechnen.
Btw die Grunfläche ist die Fläche,die den Boden darstellt. Alle Dreiecke,die zur Pyramidenspitze gehen bilden dke Mantelfläche. Und es gibt verschiedene Höhen. Die Höhe ausgegangen von der Grundfläche bis zur Spitze und die Höhe an den Seitenflächen.