Hii, kann mir jemand helfen 😅?
ich brauche eine kleine Hilfe wie ich anfangen soll bei der Aufgabe a)b)c)
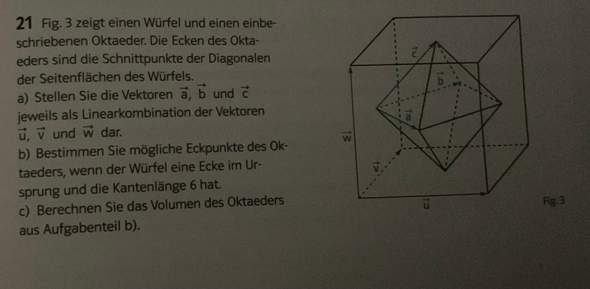
Danke im Voraus!
1 Antwort
a)
Eckpunkte des Oktaeders:
vordere Seite: Ev = 1/2*u + 1/2*w
hintere Seite: Eh = v + 1/2*u + 1/2*w
linke Seite: El = 1/2*v + 1/2*w
obere Seite: Eo = w + 1/2*u +1/2*v
jetzt kann man die Vektoren bilden (Endpunkt - Startpunkt):
Vektor a = Ev - El = (1/2*u + 1/2*w) - (1/2*v + 1/2*w) = 1/2*u - 1/2*v
Vektor b = Eh - El = (v + 1/2*u + 1/2*w) - (1/2*v + 1/2*w) = 1/2*v + 1/2*u
Vektor c = Eo - El = (w + 1/2*u +1/2*v) - (1/2*v + 1/2*w) = 1/2*w + 1/2*u
b)
Mit Kantenlänge 6 gilt:
u = (6,0,0)
v = (0,6,0)
w = (0,0,6)
vier mögliche Eckpunkte haben wir in a) bereits bestimmt:
Ev = 1/2*u + 1/2*w = (3,0,3)
Eh = v + 1/2*u + 1/2*w = (3,6,3)
El = 1/2*v + 1/2*w = (0,3,3)
Eo = w + 1/2*u +1/2*v = (3,3,6)
fehlen noch:
rechte Seite: Er = u + 1/2*v + 1/2*w = (6,3,3)
untere Seite: Eu = 1/2*u + 1/2*v = (3,3,0)
c)
Ein Oktaeder besteht aus zwei quadratischen Pyramiden mit der Grundfläche G und der Höhe h, deshalb gilt V(Oktaeder) = 2/3*G*h
Die Grundfläche der Pyramide ist die Länge des Vektors a zum Quadrat:
a = 1/2*u - 1/2*v = (3,-3,0)
Länge a = sqrt(3²+ (-3)²) = sqrt(18)
Grundfläche = sqrt(18)*sqrt(18)
Die Höhe der Pyramide ist 6/2 = 3
V(Oktaeder) = 2/3*18*3 = 36 Einheiten