Handelt es sich um eine Verstärkung?
Hi erstmal,
Ich tu mir grad etwas schwer in Physik. Nehmen wir mal an wir haben 2 harmonische Schwingungen, die die gleiche Frequenz haben und eine identische Phasenverschiebung aber unterschiedliche Amplituden...kommt es dann zu einer Verstärkung ( konstruktiven Überlagerung)?
An sich wäre das für mich das einzig logische, aber ich hätte das gerne bestätigt. Bei der online Recherche (Leifiphysik wurde Verstärkung mit Schwingungen mit gleicher Amplitude erklärt), aber ich dachte immer, dass es bei gleicher Amplitude immer zur Auslöschung kommt.
Daher bin ich grad total verwirrt.
Danke im Voraus
2 Antworten
Wenn sich zwei Schwingungen überlagern bestimmt die Phasenverschiebung wie sie sich überlagern.
Wenn beide Schwingungen gleiche Phase haben addieren sich die Amplituden, wenn beide 180° Phasendifferenz zueinander haben subtrahieren sich die Amplituden.
Also 2 Schwingungen mit Amplitude A1 und A2 ergeben bei 0 Phasendifferenz eine Schwingung mit der Amplitude A1 + A2
Haben sie 180° Phasendifferenz ergeben sie eine Schwingung mit der Amplitude A1-A2 ist nun A1=A2 erigbt A1-A2=0 und damit Auslöschung.
Ja klar. Gleiche Phase und Frequenz ist immer Verstärkung.
Für eine Auslöschung muss gleiche Frequenz gleiche Amplitude und 180° Phasenverschiebung sein
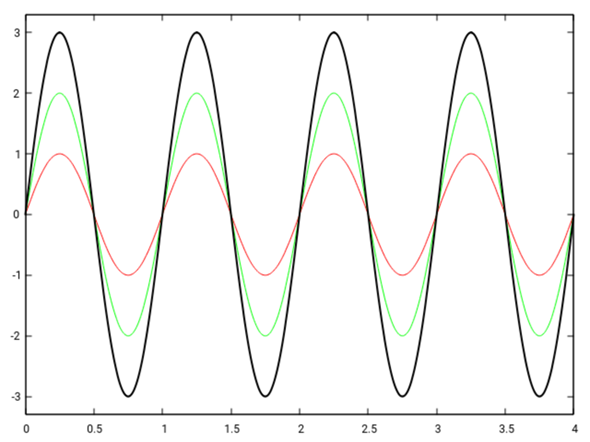
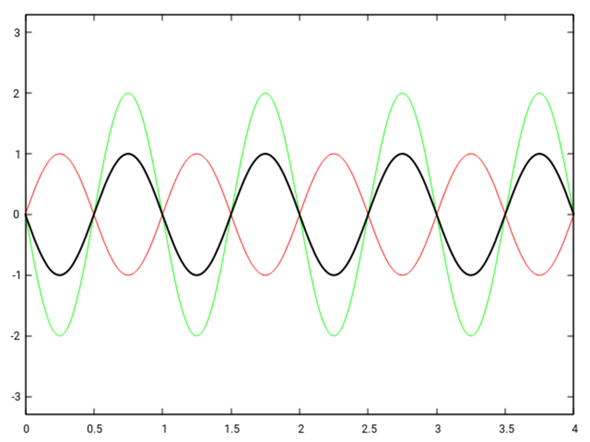
In meinen Beispiel hat die grüne Welle die doppelte Amplitude der roten. Die schwarze Kurve ist die Überlagerung von beiden. Sehen wir uns das zunächst einmal mit Phasenverschiebung Null an:
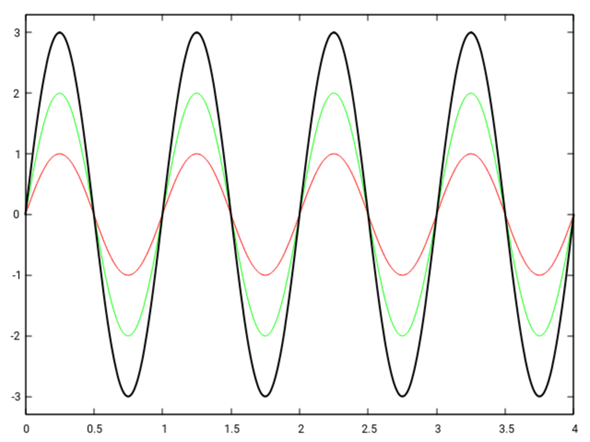
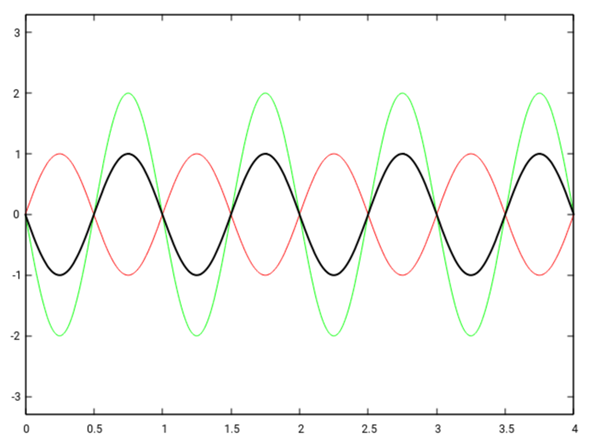
Die Interferenz ist konstruktiv. Und nun machen wir eine Phasenverschiebung von π, was zur destruktiven Interferenz führt (es bleibt also weniger Amplitude übrig):
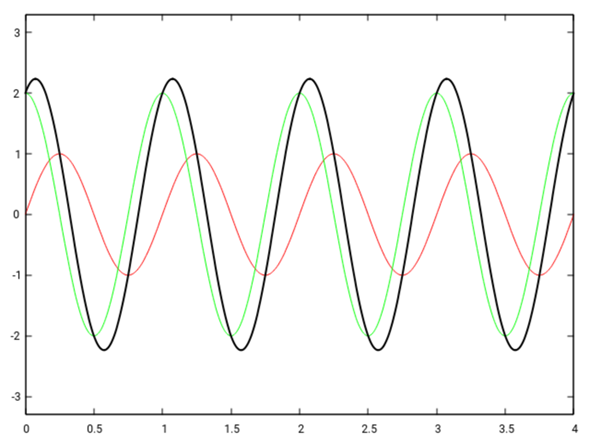
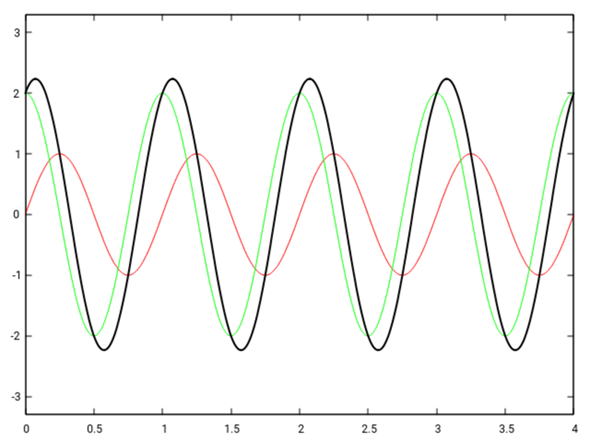
Eine x-beliebige Phasenverschiebung (z.B. π/2) führt zu einem Resultat, das in der Mitte zwischen den beiden Extremen liegt:
Ok also heisst das, dass wenn man gleicher Frequenz und Phasenverschiebung hat und gleiche Amplitude es trotzdem zur Verstärkung kommt? Also das leifiphysik recht hat?