Habe ich was falsch gemacht beim Rechnen mit den Quaternionen?
Ich habe mich aus langeweile gefragt, was in hyperkomplexen eine imaginäre Einheit hoch eine andere imaginäre Einnheit ist.
Da habe ich einfach die Einheitsquaternionen zum Rumspielen genommen, dabei kamm ich bei schon einer sehr simplen Aufgabe auf etwas, was mich verwirrt:
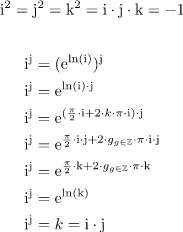
Ist da was falsch?
Es kommt mir so surreal vor, dass i hoch j (mit i, j und k als die imaginären Einheiten der Einheitsquaternionen) das gliche sein soll, wie i mal j, also "i^{j} = i * j = k".
Ist da was falsch, oder ist das wirklich so eigenartig?
Als erstes habe ich noch das aufgestellt, um zu schauen, ob ich es anwenden kann:

Woraus für jede imaginäre Einheit i_{k}: i_{k}² = -1 folgt, das sie diese Gleichung erfüllt, also k, da k² = -1, auch.
Als alternativen Rechenweg habe ich auch noch:
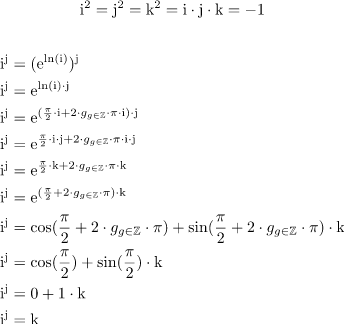
Dieser Rechenweg stützt sich auf die hergeleitete Formel, doch auch hier komme ich auf das gleiche Ergebniss...
3 Antworten
Muss nicht korrekt sein. Es ist eine mögliche Lösung.
Es könnte auch "-k" raukommen, da "ij = k" aber "ji = -k" und die Potenzregel mit der Potenz der Potenz ist die Basis hoch den eigenen Exponenten mal den anderen Exponenten.
Sie haben hier i rechtsmultipliziert mit j, wodurch k rauskam, aber machen Sie es anders rum kommen Sie auf -k.
Ich hätte dies anders gerechnet:
i = e^(i*pi/2) ; => i^j = [ e^(i*pi/2) ]^j = e^(i*pi/2)*j] = e^(k*pi/2) = k .
Es sieht für mich so aus, aber es ist über 40 Jahre her, dass ich mich mit Gruppentheorie beschäftigt habe. Es wäre denkbar, dass ich bei deiner Rechnung etwas übersehe.
Du wendest die komplexe Exponentialfunktion auf Quaternionen an - ich bin mir ehrlich gesagt im drittletzten Schritt nicht so sicher, dass du das korrekt gemacht hast.
In der dritten Zeile hast du aus Versehen k geschrieben, obwohl du g meintest. Die Schreibweise mit "g\in\Z" an g finde ich nicht so schön. Beides aber okay.
Du wendest die komplexe Exponentialfunktion auf Quaternionen an - ich bin mir ehrlich gesagt im drittletzten Schritt nicht so sicher, dass du das korrekt gemacht hast.
Ich gehe davon aus das das stimmt, da ich davor einen Beweis geschrieben/eine Fromel hergeleitet habe auf welchen das beruht:
Verallgemeinerte Eulersche Formel für alle imaginären Einheiten, für welche "i_{k}^{2} = -1" gilt:
\begin{align*}
\mathrm{e}^{x} &:= \sum_{n = 0}^{\infty} \frac{x^{n}}{n!}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \sum_{n = 0}^{\infty} \frac{(x \cdot \mathrm{i}_{k})^{n}}{n!}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \sum_{n = 0}^{\infty} \frac{x^{n} \cdot \mathrm{i}_{k}^{n}}{n!}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \sum_{n = 0}^\infty\frac{x^{2 \cdot n} \cdot \mathrm{i}_{k}^{2 \cdot n}}{(2 \cdot n)!} + \sum_{n = 0}^\infty \frac{x^{2 \cdot n + 1} \cdot \mathrm{i}_{k}^{2 \cdot n + 1}}{(2 \cdot n + 1)!}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \sum_{n = 0}^\infty \mathrm{i}_{k}^{2 \cdot n} \cdot \frac{x^{2 \cdot n}}{(2 \cdot n)!} + \sum_{n = 0}^\infty \mathrm{i}_{k}^{2 \cdot n + 1} \cdot \frac{x^{2 \cdot n + 1}}{(2 \cdot n + 1)!}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \underbrace{\sum_{n=0}^\infty (-1)^{n} \cdot \frac{x^{2 \cdot n}}{(2 \cdot n)!}}_{\cos(x)} + \underbrace{\sum_{n =0}^\infty (-1)^{n} \cdot \frac{x^{2 \cdot n + 1}}{(2 \cdot n + 1)!}}_{\sin(x)} \cdot \mathrm{i}_{k}\\
\mathrm{e}^{x \cdot \mathrm{i}_{k}} &= \cos(x) + \sin(x) \cdot \mathrm{i}_{k}
\end{align*}
Das ist die eulersche Formel rückwerts angewand.
Sie funktioniert für jede imaginäre Einheit für die i_{n}² = -1 gilt, welche k ist.
Zum prüfen könnte man alternatif auch die Formel:
e^{(pi / 2 + 2 * g * pi) * k} = cos(pi / 2 + 2 * g * pi) + k * sin(pi / 2 + 2 * g * pi) = 0 + k * 1 = k benutzen, welche mit der hergeleiteten Formel ebenso funktioniert.
Also hoffe ich, dass ich da nicht vollkommen versagt habe. ;owo;
In der dritten Zeile hast du aus Versehen k geschrieben, obwohl du g meintest. Die Schreibweise mit "g\in\Z" an g finde ich nicht so schön. Beides aber okay.
Ah das korrigiere ich lieber schnell...
Danke für den Hinweis.^^"
Aber ist die Rechnung korrekt?