Grafisches Ableiten (von f(x) zu f“(x)?
Hallo, ich verstehe leider gar nicht wie man grafisch ableitet? Könnte es mir jemand erklären ? Besonders schwer fällt es mir von f(x) zu f“(x) zu kommen. Es wäre nett wenn ihr euch an den Beispielaufgaben, die ich herausgesucht habe, orientieren könntet, um es mir daran zu erklären. Vielen Dank min Voraus
4 Antworten
erstmal von f nach f ' und dann von f ' nach f "
-----------------------------------------------------------------------------------
da wo f Extrema hat, hat f ' Nullstellen
da wo f steigt, verläuft f ' über der x-Achse
da wo f fällt, verläuft f ' unter der x-Achse;
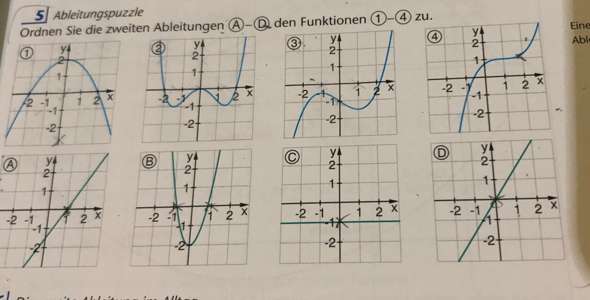
Also, 1 ist ja zweiten grades, das heißt die zweite Ableitung ist nur noch die Konstante übrig, sprich f(x) ist immer gleich, also C
2 ist vierten Grades, nach zwei Ableitungen hast du also noch zweiten Grad, eine Parabel, also B.
3 ist dritten Grades, also bleibt noch erster Grad, eine Gerade. Am Symmetriepunkt bei x=0 erkennst du, das es D sein muss, dessen Nullstelle bei x=0 ist.
4 funktioniert analog zu 3, nur, dass der Symmetriepunkt bei x=1 ist, was dann zu A passt.
Sieh dir zum Beispiel 1) an.
Du hast zuerst eine positive Steigung, dann eine Steigung von 0, dann eine negative Steigung. Also eine Gerade die vom Positiven ins Negative geht - sprich: eine konstante, negative Steigung hat. Diese Steigung ist die zweite Ableitung, deswegen ist hier die Antwort 3)
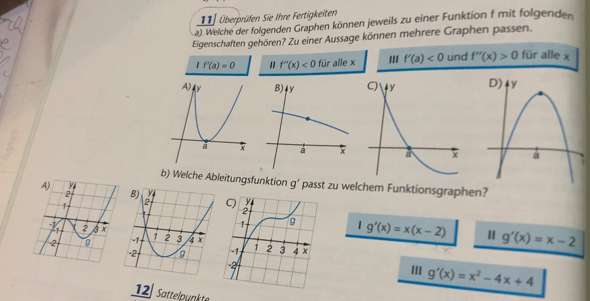
mal C gucken :
eine waagreche Gerade : heißt : der Wert für alle X ist gleich . Das heißt der Graph der ersten Ableitung muss eine Gerade ( nicht waagrecht ) gewesen sein . Denn diese hat ja überall dieselbe Steigung m !
Und zu dieser 1sten Ableitung kann nur eine Parabel passen , denn deren Ableitungsfunktion ist eine Gerade ( z.b -3x , wenn y = -1.5x² + 3 ) war .
Der Wert ist hier immer -1 , dh die 1ste Ableitung hat ein Minuszeichen , was auf eine Parabel der Form -ax² + bx + c hindeutet . Und weil der Wert -1 ist , muss vorher -0.5x² dagestanden haben .
Demnach kommt glasklar nur Graph ((1)) in Frage.
mal B gucken :
zwei Nst , daher muß die Ableitung x² haben.
die erste Ableitung x³ und die Fkt x^4 .
Die Fkt könnte also 4 NSt haben. Das kann nur ((4)) sein , obwohl dort nur 3 NSt sind . Liegt daran , dass bei 0 eine doppelte NSt ist.
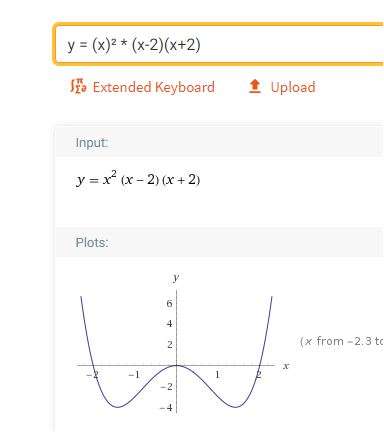
die Fkt muss also die Gleichung x²*(x-2)*(x+2) haben ..
Probe
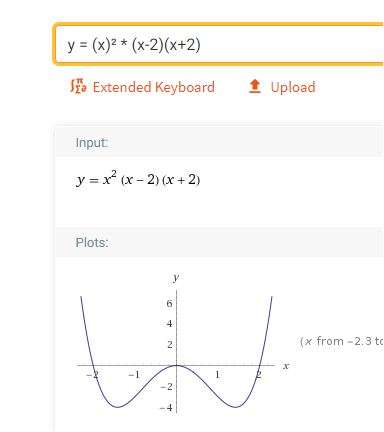
passt bist auf die Extrema mit ( x / -1 )
darum ist (1/4)*x²*(x-2)*(x+2) die Fkt-Glg.
außerdem sagen die 2 NSt in B , dass es 2 Wendepunkte geben muss , passt auch .
Und die erste Abl muss 3 NSt haben >>> 3 Extrempunkte.