Globalverhalten / Grenzverhalten?
Wie berechne ich das von dieser Funktion?
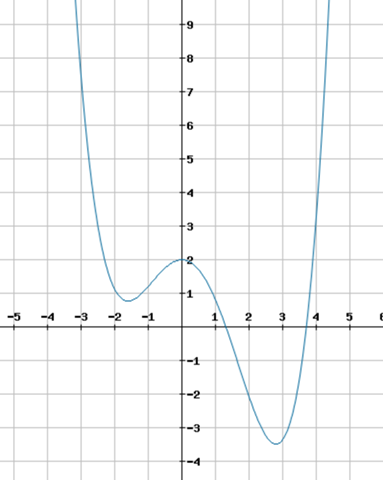
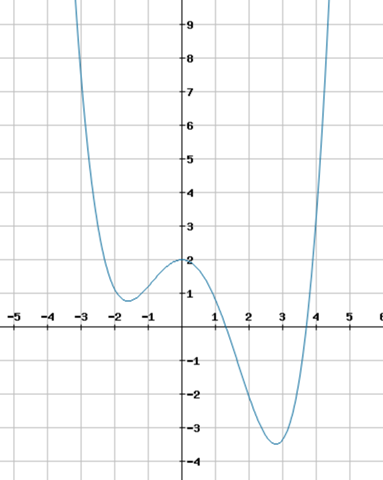
f(x) = 1/8x^4 - 1/5x^3 - 28/25x^2 + 2
1 Antwort
Wichtig ist hier die höchste Potenz, bezogen auf den Exponenten. Das ist (1/8)x⁴. Diese dominiert den Rest, weswegen der Rest der Funktion irrelevant für die Grenzwertbestimmung ist.
Nun kannst du diese Potenz gegen -∞ und +∞ laufen lassen (und falls notwendig auch gegen 0).
Fangen wir mit -∞ an. Du kannst hier einfach mal -1 einsetzen. Das reicht meisten schon aus. Dir sollte klar sein, dass eine negative Zahl mit einem geraden Exponenten (hier 4) eine positive Zahl ergibt, da - mal - wiederum + ist:
(-1)⁴ = 1
Beachte die Klammern. Das Minus wird mit potenziert.
Somit ist klar, dass die Funktion für x-> -∞ positiv ist, das Ergebnis der Grenzwertberechnung also +∞ ist.
Das bedeutet, die Funktion kommt von links oben.
Das gleiche passiert für x-> +∞. Auch 1*1*1*1 ergibt eine positive Zahl.
Das heißt: Die Funktion kommt von links oben und läuft auch rechts wieder nach oben.
Hier auch einmal der Graph zur Funktion f, welcher das Vorgehen bestätigt: