Frage zu Mathe Lösungen (Potenzen Kürzen)?
Ich übe gerade für die Abschlussprüfung Mathematik, jedoch bin ich bei einer Aufgabe auf ein Problem gestoßen. Ich verstehe den Lösungsweg, der im Buch gegeben ist, nicht. Spezifisch verstehe ich nicht wie einige Zahlen rausgekürzt wurden. Ich habe aus gesundheitlichen Gründen sehr viel in der Schule gefehlt und habe daher nicht alle Regeln dazu mitbekommen und konnte sie mir dieses Mal nicht erschließen. Im Bild sichtbar, ist die Aufgabe die mir Probleme bereitet. Zwar wird hier die 9 (übrig 3), 4, 6 und 2 weggekürzt. Jedoch verstehe ich die Regel dahinter nicht. Wenn man vom 9 mit 6 kürzt bleiben 3 übrig? Wie ist es dann bei 4? Da passt die 2 zweimal rein. Ich verstehe einfach nicht wie 3 übrig bleibt und nichts anderes, gibt es eine Regelung dass man eine Zahl weg kürzen darf wenn sie genau reinpasst? Halp
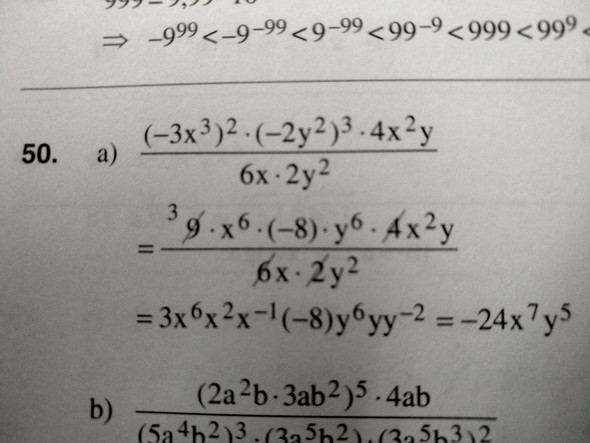
4 Antworten
Die 9 und 6 wurden zunächst durch 3 gekürzt, bleibt im Zähler 9:3=3 und im Nenner 6:3=2 übrig. Jetzt wurde die 4 hinten im Zähler mit den beiden 2en im Nenner komplett weggekürzt.
Ich hätte aber auch direkt x und y² aus dem Nenner mit z. B. x^6 und y^6 aus dem Zähler gekürzt, statt im nächsten Schritt die Potenzen des Nenners umzuformen in Potenzen mit negativem Exponenten, um dann die Potenzen zusammenzufassen...
Hallo,
beachte folgende Regeln:
Exponenten gehören nur zu der Zahl oder Variablen, mit der sie direkt verbunden sind, es sein denn, sie stehen hinter einer Klammer:
ab²=a*b*b, nicht a*a*b*b
Aber:
(ab)²=a*b*a*b=a²b²
Wenn eine Potenz potenziert wird, wird die Basis beibehalten und die Exponenten werden multipliziert:
(a²)³=a^(2*3)=a^6
Dividierst Du zwei Potenzen mit gleicher Basis, werden die Basen beibehalten und die Exponenten dividiert:
a³/a²=a^(3-2)=a^1=a
Multiplizierst Du zwei Potenzen mit gleichen Basen, werden die Basen beibehalten und die Exponenten addiert:
a²*a³=a^(2+3)=a^5
Faktoren, die aus Zahlen bestehen, kannst Du ganz einfach miteinander multiplizieren oder durcheinander dividieren oder addieren oder subtrahieren.
Das Letztere geht nur, wenn das, was nach den Zahlen kommt, gleich ist:
3ab²+2ab²=5ab²
aber:
3a²b+2ab² kannst Du nicht addieren. Du kannst auch keine 3 Hunde und 2 Katzen zu 5 Hutzen zusammenfassen oder so.
Dagegen:
3a²b*2ab² geht ohne Probleme:
Das ergibt 3*2*a²*a*b*b²=6a³b³
Wird eine Zahl mit einem Minus davor quadriert, bleibt das Minus erhalten, wenn um die Zahl und das Minus keine Klammer gesetzt ist und der Exponent außen bleibt:
-3²=-9
Aber:
(-3)²=9 (jetzt wird auch das Minus, eigentlich der Faktor (-1) mitquadriert).
Bei ungeraden Exponenten bleibt das Minus auf jeden Fall erhalten, ob mit oder ohne Klammer:
-2³=(-2)³=-8, denn Minus mal Minus mal Minus ergibt wieder ein Minus.
a^(-1)=1/a^1, a^(-2)=1/a^2 usw.
Wenn Du diese Regeln beachtest, solltest Du die Lösungen nachvollziehen können.
Herzliche Grüße,
Willy
Die 9 kann du in 3*3 aufspalten, also wird an dieser Stelle eine 3 gekürzt.
über dem Bruchstrich gekürzt: 3*4 =12
unter dem Bruchstrich gekürzt: 6*2 = 12
Ok. Gehst Du youtube, gibst Fach und Thema in die Suchmaske und erhältst kostenlosen Unterricht vom Feinsten. Können wir hier nicht gegen anstinken.
Natürlich wirst Du auch über die Suchmaske des Browsers fündig. Die dort dann angezeigten kostenlosen Seiten beinhalten in der Regel neben schriftlichem Unterricht auch ein Forum und reichlich Übungsmaterial.