Formeln der gleichmäßig beschleunigten Bewegung?

Mein Lehrer hat mir 3 Formeln gegeben, und nur mit einer kann ich etwas anfangen:

$a=\frac{v_2-v_1}{t_2-t_1},$

das verstehe ich damit kann man die Beschleunigung eines Objektes berechnen, indem man einen Anfangswert nimmt.

Also man nimmt die Geschwindigkeit am Ende - Geschwindigkeit am Anfang und das Gleiche mit der Zeit, und so bekommt man raus, um wie viel sich das Objekt in einer bestimmten Zeit beschleunigt hat (die Beschleunigung ist dabei immer konstant).

Aber was ist mit den Gleichungen:

$v=a\cdot t+v_0$

$s=\frac{at^2}{2}+v_0\cdot t+s_0$

Was haben die für ein Sinn?

Answer 1

[SlowPhil]

Hallo wissenslustly,

die Formeln sind nicht 100% konsequent formuliert, weil unterschiedliche Formelzeichen bzw. Indizes verwendet werden. Anstelle von

$(1)\quad a=\frac{v_2-v_1}{t_2-t_1}=\frac{\Delta v}{\Delta t}$

hätte man auch

$(2)\quad a=\frac{v_1-v_0}{t_1-t_0}=\frac{\Delta v}{\Delta t}$

schreiben können. Dann wären die anderen Formeln leichter verständlich. Um beispielsweise die zweite Formel zu erhalten, brauchst Du nur nach v₁ umzustellen:

$(3)\quad v_1=v_0+a(t_1-t_0)=v_0+a\cdot\Delta t$

Es ist etwas unglücklich, dass nur einfach 't' geschrieben wurde. Allgemeiner kann man allerdings auch

$(4)\quad v(t)=v_0+a\cdot(t-t_0)$

schreiben, wobei sich auch der Zeitnullpunkt willkürlich setzen lässt, also auch t₀=0. In dem Fall kommt genau die obige Formel heraus.

In einem t-v-Diagramm ist v(t) eine Gerade, die mit den Vertikalen bei t₀ und t₁ und der t-Achse ein Trapez einschließt. Dies lässt ich in ein Rechteck der Grundseite t-t₀ und Höhe v₀ und ein Dreieck derselben Grundseite und der Höhe v₁-v₀ aufteilen, und die zurückgelegte Strecke ∆x (in der Formel s) ist die Fläche dieses Trapezes

Grundseite × Höhe₀ + (Grundseite × Höhe₁)/2 = Grundseite × (Höhe₀ + Höhe₁/2),

also

$(5)\quad\Delta x=\Delta t\cdot(v_0+\frac{a\cdot\Delta t}{2})=v_0\Delta t+\frac{a\Delta t^2}{2},$

und wenn man x=x₀+∆x schreibt, hat man die obige Formel eigentlich reproduziert.

Woher ich das weiß: Studium / Ausbildung

Comments

[SlowPhil]

Danke für den Stern.

Answer 2

[UlrichNagel]

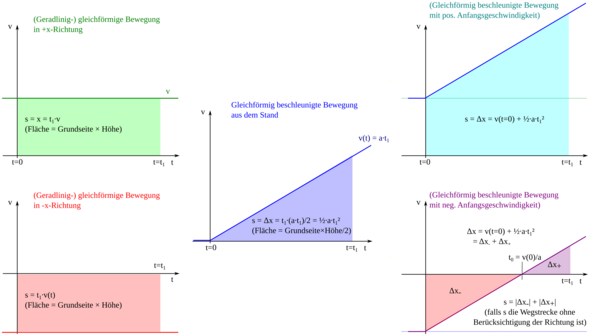
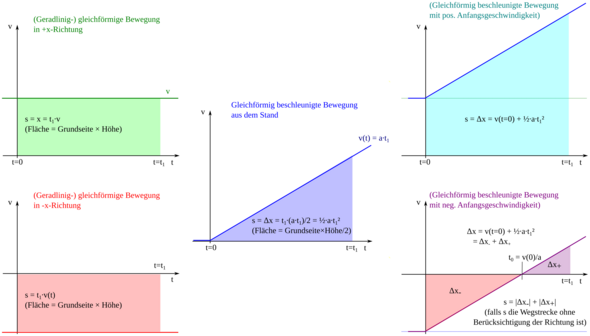
Es ist eigentlich nur eine Formel, die anderen bekommt man durch Umformung! Zeichne dir bitte die 3 Diagramme s-t, v-t und a-t! Die jeweilige Fläche unter den Kurven ist die darüberliegende Größe:

a-t: v = at + v0, falls Anfangs-v vorliegt!

v-t: s = 1/2 vt + s0 wenn Anfangsweg vorliegt! 1/2 vt ist hälfte des Rechtecks, das Dreieck!

Answer 3

[Samimind]

Geschwindigkeit:

Hast du ein Objekt mit einer konstanten Beschleunigung a und einer Anfangsgeschwindigkeit v0 (zb. Freier Fall mit a=9.81m/s²) kannst du mit

$v=at+v_0$ die Geschwindigkeit nach der Zeit t berechnen.

--------------------------------------------------------------------------------------------------------------------------------

Strecke:

Hast du ein Objekt mit einer konstanten Beschleunigung a einer Anfangsgeschwindigkeit v0 und einem Anfangsweg s0 kannst du mit

$s=\frac{at^2}{2}+v_0t+s_0$

die Strecke nach der Zeit t herausfinden.

--------------------------------------------------------------------------------------------------------------------------------

Zusatz: (nur wenn du Ableitungen und Stammfunktionen kennst)

Hier noch was zum Verständnis:

$a\left(t\right)=v'\left(t\right)=s''\left(t\right)$

-> Heißt du kannst dir die Formeln also so herleiten:

$v\left(t\right)=\int adt=at+C$ $s\left(t\right)=\int v\left(t\right)\mathrm{d}t=\frac{at^2}{2}+v_0t+C$

Woher ich das weiß: Studium / Ausbildung

Answer 4

[Tannibi]

Bescheinigung eines Objektes 

Auto-Vervollständigen wird immer lustiger.