Eulersche Identität verstehen?
Ich beschäftige mich grade mit den komplexen Zahlen aber verstehe die Formel e^iπ=-1 nicht. Ich hatte bis jetzt auch noch keine exponentialfunktionen in der Schule, also fehlen mir vielleicht ein paar Grundkenntnisse um die Formel wirklich zu verstehen. Kann mir jemand ungefähr sagen, mit welchen Themen ich mich vorher beschäftigen muss um sie zu verstehen?
3 Antworten
Hat eigentlich gar nicht viel mit der Exponentialfunktion selbst zu tun, eher mit dem Fakt der Reihenentwicklung der Funktion. Diese ist mit dem Argument ix „zufällig“ genau das gleiche wie die Reihen von cos(x) zusammen mit i*sin(x).
Die Zahlenebene für komplexe Zahlen hattest du ja schon. Also auf der y-Achse ist die imaginäre Einheit und auf der x-Achse der reale Teil.
Das bedeutet, wenn ich eine Bogenlänge (einen Winkel) für x bei e^(ix) einsetze, wird die y-Koordinate durch den Sinus davon und die x-Koordinate durch den Cosinus bestimmt (also in der Zahlenebene).
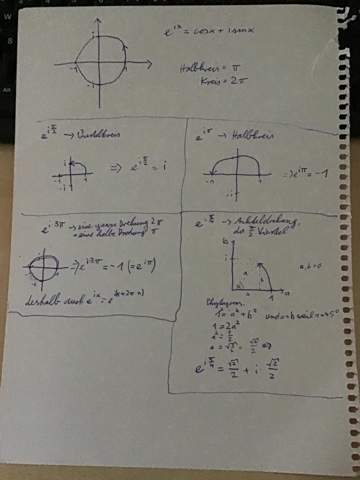
Das bedeutet, für alle Werte von x ergibt sich tatsächlich ein Einheitskreis mit dem Radius 1 um den Ursprung. Wenn ich einen Viertelkreis gehe, als x=pi/2, dann bekomme ich i. Wenn ich mich einen Halbkreis drehe, also x=pi, dann komme ich bei -1 an. e^(2pi*i) ist dementsprechend eine ganze Drehung also 1.
Das ist eigentlich schon das ganze Geheimnis der Formel e^(ix). Bisschen schwer zu verstehen aber wenn man es einmal hat ist es einfach ein tolles Tool, auch in der reellen Mathematik.
Das Video kannst du dir zur e-Funktion mit der Reihenentwicklung anschauen:
Insgesamt ist also meiner Meinung nach zum Verstehen nur wichtig, warum e^(ix)=cos(x)+isin(x). Dann sollte man verstehen, dass das bedeutet dass man sich mit dem Verändern von x um den Einheitskreis dreht.
Ich hoffe das hilft dir weiter! Aber da du Exponentialfunktionen noch gar nicht in der Schule hattest ist ja noch viel Zeit zum Verstehen 😅

Schau Dir die Gaußsche Zahlenebene an und beschäftige Dich mit komplexen Zahlen. Insbesondere auch mit Polarkoordinaten/Polarform.
Bedenke, der Umfang des Einheitskreises ist 2Pi im Bogenmaß, was bedeutet, Pi ist ein Halbkreis.
https://de.wikipedia.org/wiki/Komplexe_Zahl#Komplexe_Zahlenebene
NAchtrag, die Eulersche Relation nicht vergessen:
du hast ja genau das gefragt. Jetzt hast du noch nie gehört davon?
Ja, habe mir den Link angeschaut. Mir war lediglich die Bezeichnung nicht bekannt :‘(
Mit Taylor-Reihenentwicklungen, sin und cos und der Zahl e.
Beweise findest du im Internet tausende.
Die gaußsche Zahlenebene und die polarkoordinaten habe ich mir schon angeschaut :) Von der eulerschen Relation habe ich bisher nichts gehört, vielen Dank !