Schnittpunkt ausrechnen (Ebenen)?
Einen schönen Abend wünsche ich erstmals.
Um mich für meine Klausuren vorzubereiten habe ich mir einige Übungen vorgenommen und bin auf eine gestoßen, wo ich große Schwierigkeiten habe.
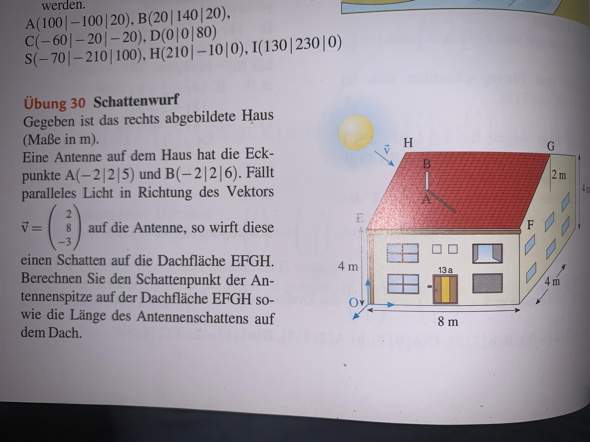
1) Eine Ebenengleichung für die Dachfläche aufstellen und die Parameterform in die Koordinatenform stellen. ( Vektor "v" ist der Richtungsvektor, B ein Stützvektor)
Berechne den Schnittpunkt von g | E.
Ich weiß weder den Ansatz, noch die Lösung. Ich bitte um Hilfe.
2 Antworten
Dreipunktgleichung der Ebene E: x=a+r*(b-a)+s*(c-a)
A(ax/ay/az) → Ortsvektor a(ax/ay/az)
E(0/0/4) nehmen wir als A(0/0/4) → a(0/0/4)
F(0/8/4) nehmen wir als B(0/8/4) → b(0/8/4)
G(-4/8/6) nehmen wir als C(-4/8/6) → c(-4/8/6)
eingesetzt und ausgerechnet ergibt das die Vektorielle Parametergleichung der Ebene.
E: x=a+r*u+s*v
u=b-a
v=c-a
Daraus kann man die Normalengleichung der Ebene berechnen
E: (x-a)*n=0
den Normalenvektor n(nx/ny/nz) kann man aus den Richtungsvektoren u(ux/uy/uz) und v(vx/vy/vz) berechnen
Skalarprodukt a*b=ax*bx+ay*by+az*bz=0
Normalenvektor n(nx/ny/nz) steht senkrecht auf den Richtungsvektoren u und v
ergibt das lineare Gleichungssystem
1) nx*ux+ny*uy+nz*uz=0
2) nx*vx+ny*vy+nz*vz=0
wir setzen nz=1
1) nx*ux+ny*uy=-1*uz
2) nx*vx+ny*vy=-1*vz
die beiden Unbekannten sind nx und ny weil wir ja nz=1 gesetzt haben
Stützpunkt der Ebene nehmen wir mit Punkt A(-2/2/5) → a(-2/2/5)
Ebene (x-(-2/2/5)*(nx/ny/nz)=0
Geradengleichung von der Antenne aus B(-2/2/6) → b(-2/2/6)
g: x=(-2/2/6)+t*(2/8/-3)
eingesetzt mit der Ebene
[(-2/2/6)+t*(2/8/-3)-(-2/2/5)]*(nx/ny/nz)=0
Skalarprodukt anwenden a*b=ax*bx+ay*by+az*bz=...
ausmultiplizieren und zusammenfassen und dann nach den Parameter t=... umstellen ergibt den Schnittpunkt mit der Ebene
Abstand von 2 Punkten im Raum Betrag |d|=Wurzel((x2-x1)²+(y2-y1)²+(z2-z1)²)
Punkt A(-2/2/5) nach Schnittpunkt (x/y/z)=(-2/2/6)+t*(2/8/-3)
Den Rest schaffst du selber.Ist nicht besonders schwer,aber viel Rechnerei und das Risiko für Rechenfehler ist hoch.
Soory mach sie liber selber wenn eine Arbeit kommt dan kannst du nicht 👇
Naja, ich würde sie ja gerne machen wenn ich die Aufgabe verstehen würde, bzw. den Ansatz wüsste. Da dies nicht der Fall ist, suche ich hier nach Hilfe. :)
Das wird mehr deutlich helfen. Vielen Dank