Dreieck konstruieren mit Seitenhalbierenden?

Hallo wie konstruiere ich ein Dreieck bei dem 3 Angaben gegeben sind. 2 Seitenhalbierende und eine strecke.

Answer 1

[jeanyfan]

Ich hab dir hier mal ne Zeichnung dazu gemacht:

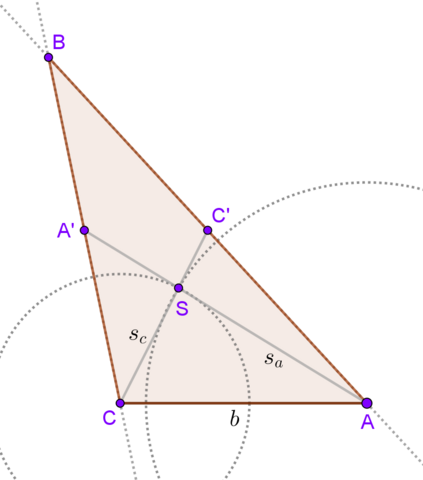
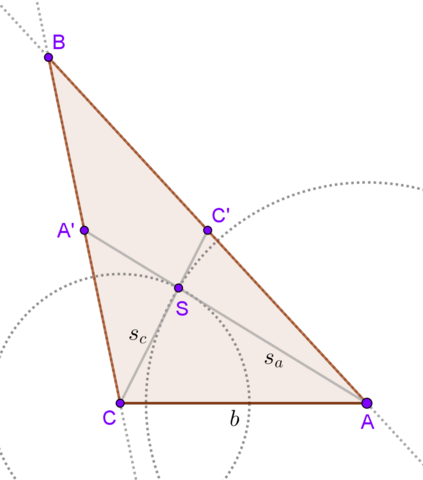
Wichtig ist zu wissen, dass sich die drei Seitenhalbierenden im Verhältnis 2:1 im Schwerpunkt S schneiden. Der längere Teil (also 2/3 der Seitenhalbierenden) liegt zwischen dem Eckpunkt und S, 1/3 zwischen S und dem Mitte der Seite.

Erst zeichnest du die Seite b und dann zwei Kreise mit jeweils 2/3 der entsprechenden Seitenhalbierenden als Radius um A (Radius (2/3)* s_a) und C (Radius (2/3)* s_c). Der Schnitt beider Kreise ist S.

Dann zeichnest du von A durch S die ganze Seitenhalbierende s_a (ergibt A') und von C durch S die ganze Seitenhalbierende s_c (ergibt C').

Von A durch C' und von C durch A' zeichnest du zwei Geraden.

Der Schnittpunkt dieser zwei Geraden ist B.

Comments

[Enis2744]

Wie teile ich die seitenhalbierende jn 3 Stücke?

[jeanyfan]

@Enis2744

Einfach die Länge geteilt durch 3.

Wenn du dann 2/3 davon als Radius willst, entweder den Wert geteilt durch 3 und danach mal 2. Oder direkt den Wert mal (2/3).

[Enis2744]

Darf ich statt C’ und A’ auch einfach a und c nehmen?

[jeanyfan]

@Enis2744

Das sollen ja Punkte sein, a und c sind ja deine Seitenlängen.

A' ist eben grade die Mitte der Seite A und C' die Mitte der Seite c.

Kannst sie aber z.B. auch M_a und M_c nennen.

[jeanyfan]

@jeanyfan

Hast es eigentlich verstanden, wie ich das Dreieck konstruiert habe dann?

Answer 2

[Dreamlight]

Du müsstest es schon genauer beschreiben was du genau hast

Answer 3

[jeanyfan]

Welche Strecke und welche Seitenhalbierenden hast du genau?

Comments

[Enis2744]

b=7cm sa=9,4cm sc=5,5cm

[schmidtmechau]

@Enis2744

Du kannst doch wohl Deine beiden Seitenhalbierenden in Drittel teilen! Das kann man doch im Kopf rechnen!

2/3 sa = 2/3 * 9,4 = 6,26667

2/3 sc = 2/3 * 5,5 = 3,66667

[Enis2744]

Beim konstruieren...