Differentialrechnen mit mehreren Variabeln; Fehlerfortpflanzung?
Hallo Zusammen, kann mir bitte jemand bei folgender Aufgabe helfen, was ich hier falsch gemacht habe:
Ein Dreieck mit der Seite c ? 103.m und den Winkeln alpha = 50 gon und gamma = 35gon sind gegeben. Die Standartabweichungen betragen sigma(c) = 3cm, sigma(alpha) und sigma(gamma) = je 1mgon.
Die Seite c wurde dabei 6x gemssen, alpha 4x und gamma 7x.
------------------------------------------------------------------------------------------------------------
a) bestimme die Formel für die Berechnung der Seite a.
für a) habe ich den Sinussatz angewendet.
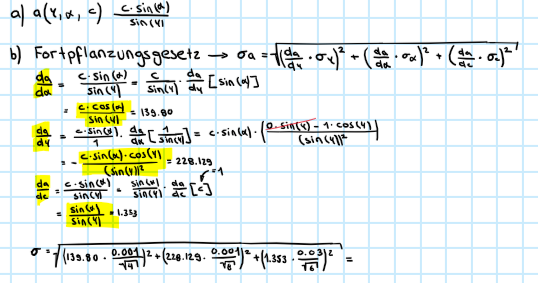
b) Schätze die Standartabweichung der Seite a ab.
Wie muss ich hier vorgehen?
-------------------------------------------------------------------------------------------------
Die Lösung sollte "c sigma +/- 1.67cm" sein. (wieso "c" weiss ich ebenfalls ncht, wenn in der Aufgabe nach der Seite a gesucht wird, aber nehme mal an, dass das ein Tippfehler ist.
In Wolframalpha erhalte ich folgende Lösung:
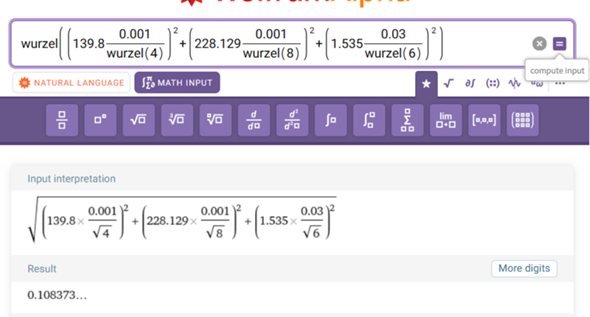
Ich danke euch für eine Rückmeldung.
2 Antworten
In der Aufgabenformulierung ist einiges unklar. Gilt exakt c = 103.0 cm oder meter ? Denn damit erhalte ich für den α-Fehler ~ 139.39 und für den γ-Fehler 227.47
Abgesehen davon sind die 1mgon in der Abschätzung falsch, man muss steht dessen das Bogenmass = 0.001*pi/200 einsetzen.
Ausserdem ist vermutlich die 0.03 falsch und muss durch 3 ersetzt werden. Es sei denn die c = 103 wären Meter. Aber damit kann die Lösung auf keinen Fall stimmen.
In der Aufgabenformulierung wurde γ sieben mal gemessen, warum steht dann in der Abschätzung sqrt(8) ?
Mit den geänderten Werten ergibt sich die Abschätzung zu ~ 1.66
Hinweis:
Die Standardabweichung in Gon muss in Bogenmaß umgerechnet werden, also durch ρ = 200 Gon / π dividiert werden.
σ_a = √(((sin(α) / sin(γ)) * σ_c)² + ((c * cos(α) / sin(γ)) * σ_α)² + ((-c * sin(α) * cos(γ) / sin²(γ)) * σ_γ)²)
σ_a = √(((sin(50 Gon) / sin(35 Gon)) * 0,03 m / √(6))² + ((103 m * cos(50 Gon ) / sin(35 Gon)) * (0,001 Gon / (200 Gon / π)) / √(4))² + ((-103 m * sin(50 Gon) * cos(35 Gon) /sin²(35 Gon)) * 0,001 Gon / (200 Gon / π) / √(7))²)
σ_a = √((0,0165747 m)² + (0,00109478 m)² + (0,00135048 m)²)
σ_a = +-0,0167 m
σ_a = +-1,67 cm